pairing-based-crypto

What is pairing?

 最近在搞中期报告，要用到一些双线性配对密码学的知识。我们都知道双线性配对满足一些计算性质，例如$e(u^a,v^b)=e(u,v)^{ab}$，利用双线性配对可以构造很多密码学算法，当然也是身份加密的基础。然而，双线性配对到底是啥呢？咋来的呢？具体应用是什么呢？

 首先要引入一些概念。

 群。一种代数结构，由一组元素和二元运算*组成。群必须满足以下四个条件：

  • 封闭性：对于群中的任意两个元素 a 和 b，a*b 仍在群中。
  • 结合性：对于群中的任意元素 a、b 和 c，有 (a∗b)∗c=a∗(b∗c)。
  • 单位元：存在一个单位元 e，使得对于任何元素 a，都有 a∗e=a。
  • 逆元：对于群中的每个元素 a，存在一个元素 b，使得 a∗b=e。

 离散对数问题（DLP）。给定一个加法群 G，P 是 G 的生成元，群的阶为 n，以及一个群中的元素 Q。DLP 是要求找到一个整数 $x \in [0,n−1]$，使得：Q=x*P。当 n 很大的时候，而且群如果是精心选择的话，DLP 很困难。

 Diffie-Hellman 问题（DHP）。给定 P、aP 和 bP 的情况下得到 abP。很容易看出来 DHP 比 DLP 简单，因为多了一些信息。

pairing 是怎么来的？

 给一个域 K 上的椭圆曲线 E：$y_2 + a_1xy + a_3y = x_3 + a_2x_2 + a_4x + a_6$，其中 $a_1,a_2,a_3,a_4,a_6 \in K$。E(K) 是一个点集，由无穷远处的点和满足上式的点 $(x, y) \in K * K$ 组成。假设 K 是阶数为 q、特征为 p 的有限域 $F_q$，那么 E(K) 中的元素数量$#E(K)$满足：${(\sqrt{q}-1)}^2 \leq #E(K) \leq {(\sqrt{q}+1)}^2$（Hasse 定理），可以推导出$#E(K) = q + 1 − t$，其中$|t| \leq 2 \sqrt{q}$。如果 $p | t$ ，则 E 被称为超奇异，否则 E 是普通的。如果 q 是素数，那么对于每个 t，$|t| < 2 \sqrt{q}$，都存在一条在 $F_q$ 上定义的椭圆曲线 E，其中 $#E(F_q) = q + 1 − t$。

 如果 p > 3，则 E 转换为：$y^2 = x^3 + ax + b$，其中 $a, b \in K$ 且 $4a^3 +27b^2 \ne 0$。如果 E 是超奇异且 p = 3，则 E 转换为：$y^2 = x^3 + ax + b$，其中 $a, b \in K$ 且 $b \ne 0$。如果 E 是超奇异且 p = 2，则转换为：$y^2 + cy = x^3 + ax + b$，其中 $a, b, c \in K$ 且 $c \ne 0$。下面是椭圆曲线的计算规则：

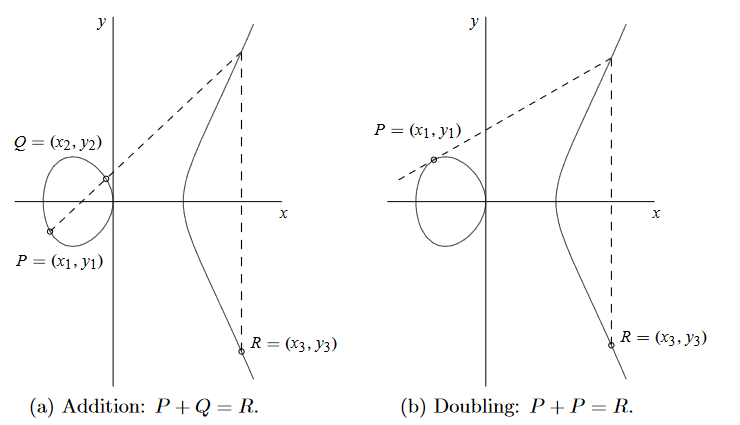
image-20241204141756488

 令 $P \in E(K)$ 为素数阶 n 的点，并假设 gcd(n, q) = 1。P 中的椭圆曲线离散对数问题（ECDLP）如下：给定 $P,Q \in〈P〉$，找到整数 $l$ 使得 $Q = lP$。已知用于求解 ECDLP 的最佳通用算法是 Pollard 的 rho 方法，时间复杂度为 $O(\sqrt{n})$。Weil 和 Tate 配对可用于将 ECDLP 实例转换为扩展域 $F{q^k}$ 中的离散对数问题。令 E 为在 $F_q$ 上定义的椭圆曲线，$P \in E(F_q)$ 为素数阶 n 的点。假设 gcd(n, q) = 1。则 P 的嵌入度是满足 $n|q^k-1 $ 的最小正整数 k。如果嵌入度 k 较小，则用于求解 $F{q^k}$ 中的 DLP 可能比用于求解 ECDLP 更快。

 人们一致认为，低嵌入度的椭圆曲线不应在离散对数协议中使用，因为会受到 Weil 和 Tate 配对攻击。然而，低嵌入度椭圆曲线现在又重新流行起来，因为它们可以实现基于配对的协议。

 那什么是 Weil 和 Tate 配对攻击呢？令 E 是在 $K = Fq$ 上定义的椭圆曲线，并令 $K’$ 表示 K 的代数闭包，用 $E(K’)$ 表示 E。E 上的除数是 $D = \sum{P \in E}{n_P(P)}$，其中 $n_P$ 是整数集。如果对于 K 的所有自重构 $\alpha$，满足 $D^\alpha=\sum_P{n_P(P^\alpha)}=D$，$P^\alpha=(\alpha(x), \alpha(y))$，那么就叫 D 在 K 上定义了。在 K 上定义的所有除数的集合用 $Div_K (E)$ 表示。

The Weil Pairing

设 $E/\mathbb{F}q$ 为一条椭圆曲线，其点群包含一个阶为 $r$ 的循环群。令 $k$ 为使 $\mathbb{F}{q^k}$ 包含 $r$ 个单位根的最小整数。$fP$ 表示除数为 $l(P)-l(O)$ 的有理函数，而 $A_P$ 表示相当于 $P-O$ 的除数。Weil Pairing $E[r] * E[r] \rightarrow \mathbb{F}{q^k}$ 可以定义为：$e(P,Q) = f_P(A_Q)/f_Q(A_P)$。Miller 算法用于计算 $f_P(A_Q)$。因此，如果我们能找到某个点 $P$ 和一个同态 $\alpha :P \rightarrow E[r]$，使得 $\alpha(P)$ 和 $P$ 线性独立，则可得到适用于密码学的双线性配对，其中定义：$f(P,Q) = e(P, \alpha(Q))$。

举个例子，假设 $q=3, p=4, E:y^2=x^3+x$。令 $r$ 为整除 $q+1$ 的最大素数，定义 $h$ 为 $rh=q+1$。则 $E(\mathbb{F}_q)$ 包含一个 $r$ 阶循环子群，我们称之为 $G$。考虑由 $\alpha(x,y)=(-x,iy)$ 给出的同态 $\alpha : E(\mathbb{F}{q})\rightarrow E(\mathbb{F}{q^2})$。至此，我们有一个双线性非退化配对的具体例子，该群上的离散对数被广泛认为是困难的。

The Tate Pairing

假设 $E$ 是定义在有限域 $K$ 上的椭圆曲线，$K$ 包含 $r$ 次单位根。Tate pairing $e: E[r] \cap E(K)E(K)/rE(K) \rightarrow K^/K^{*r}$ 可以定义为：$e(P,Q)=f_P(A_Q)$。

Miller algorithm

假设 $g{P,Q}$ 为点 $P$ 和 $Q$ 连的直线，假设 $f_c$ 为除数为 $c(P)-(cP)-(c-1)(O)$ 的函数。那么对于所有 $a,b$，我们有 $f{a+b}(Q)=fa (Q)f_b (Q)g{aP,bP}(Q)/g_{(a+b)P,-(a+b)P}(Q)$。假设 $l$ 的二进制表示为 $l_t,..,l_0$。那么 Miller 算法计算 $f_P(Q)$ 如下：

  • 设置 $f=1, V=P$。
  • 对于 $i=t-1,..,0$，计算：$f=f^2g{V,V}(Q)/g{2V,-2V}(Q), V= 2V$。若 $li=1$，就计算：$f=fg{V,P}(Q)/g_{V+P,-V-P}(Q), V= P+V$。
  • 最终有 $f=f_l(Q)=f_P(Q),V=lP=O$。

 通过在上述算法中添加额外的逻辑，我们可以避免在计算 $g$ 函数时处理无穷远点。在最后一次迭代中，如果 $l$ 为奇数，我们知道 $V=-P$，如果 $l$ 为偶数，则 $V$ 的阶为 2。下面计算 $g_{P,Q}$，假设曲线为 $y^2=x^3+a*x+b$：

  • 切线：在点 $(x,y)$，描述该点的切线的线是 $-\beta X+Y+(-y+\beta*x)$，其中 $\beta = (3x^2+a)/2y$。
  • 垂直线：这些是 $P$ 和 $-P$ 之间的线。设 $P=(x,y)$。则通过 $P$ 的垂直线为 $X-x$。
  • 其它的线：在点 $P=(x_1,y_1)$ 与 $Q=(x_2,y_2)$ 的线是 $-\beta X+Y+(-y_1+\beta*x_1)$，其中 $\beta = (y_2-y_1)/(x_2-x_1)$。

 上述函数可以缩放，结果为：

  • 切线：$-(3x^2+a)X+2yY+(-2y^2+x(3x^2+a))$。
  • 垂直线：$X-x$。
  • 其它的线：$(y_1-y_2)X+(x_2-x_1)Y+(x_1y_2-x_2y_1)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
static void miller(element_t res, element_t P, element_ptr QR, element_ptr R, int n) {
  // Collate divisions.
  mp_bitcnt_t i;
  element_t v, vd;
  element_t V;
  element_t a, b, c;
  const element_ptr cca = curve_a_coeff(P);
  const element_ptr Px = curve_x_coord(P);
  const element_ptr Py = curve_y_coord(P);
  element_t e0, e1;
  mpz_t r;
  element_ptr Vx, Vy;
  const element_ptr QRx = curve_x_coord(QR);
  const element_ptr QRy = curve_y_coord(QR);
  const element_ptr Rx = curve_x_coord(R);
  const element_ptr Ry = curve_y_coord(R);

  #define do_vertical(e, edenom) {       \
    element_sub(e0, QRx, Vx);            \ // e0 = QR.x - V.x
    element_mul((e), (e), e0);           \ // e = e * (QR.x - V.x)
                                         \
    element_sub(e0, Rx, Vx);             \ // e0 = R.x - V.x
    element_mul((edenom), (edenom), e0); \ // edenom = edenom * (R.x - V.x)
  }

  #define do_tangent(e, edenom) {                  \
    /*a = -slope_tangent(A.x, A.y);                \
      b = 1;                                       \
      c = -(A.y + a * A.x);                        \
      but we multiply by 2*A.y to avoid division*/ \
                                                   \
    /*a = -Ax * (Ax + Ax + Ax + twicea_2) - a_4;   \
      Common curves: a2 = 0 (and cc->a is a_4), so \
      a = -(3 Ax^2 + cc->a)                        \
      b = 2 * Ay                                   \
      c = -(2 Ay^2 + a Ax);                     */ \
                                                   \
    if (element_is0(Vy)) {                         \
      do_vertical((e), (edenom));                  \
    } else {                                       \
      element_square(a, Vx);                       \ // a = Vx^2
      element_mul_si(a, a, 3);                     \ // a = 3 * Vx^2
      element_add(a, a, cca);                      \ // a = 3 * Vx^2 + curve_a
      element_neg(a, a);                           \ // a = -(3 * Vx^2 + curve_a)
                                                   \
      element_add(b, Vy, Vy);                      \ // b = 2 * Vy
                                                   \
      element_mul(e0, b, Vy);                      \ // e0 = b * Vy
      element_mul(c, a, Vx);                       \ // c = a * Vx
      element_add(c, c, e0);                       \ // c = a * Vx + 2 * Vy * Vy
      element_neg(c, c);                           \ // c = -(a * Vx + 2 * Vy^2)
                                                   \
      element_mul(e0, a, QRx);                     \ // e0 = a * QR.x
      element_mul(e1, b, QRy);                     \ // e1 = b * QR.y
      element_add(e0, e0, e1);                     \ // e0 = a * QR.x + b * QR.y
      element_add(e0, e0, c);                      \ // e0 = a * QR.x + b * QR.y + c
      element_mul((e), (e), e0);                   \ // e = e * e0
                                                   \
      element_mul(e0, a, Rx);                      \ // e0 = a * R.x
      element_mul(e1, b, Ry);                      \ // e1 = b * R.y
      element_add(e0, e0, e1);                     \ // e0 = a * R.x + b * R.y
      element_add(e0, e0, c);                      \ // e0 = a * R.x + b * R.y + c
      element_mul((edenom), (edenom), e0);         \ // edenom = edenom * e0
    }                                              \
  }

  #define do_line(e, edenom) {         \
    if (!element_cmp(Vx, Px)) {        \
      if (!element_cmp(Vy, Py)) {      \
        do_tangent(e, edenom);         \
      } else {                         \
        do_vertical(e, edenom);        \
      }                                \
    } else {                           \
      element_sub(b, Px, Vx);          \
      element_sub(a, Vy, Py);          \
      element_mul(c, Vx, Py);          \
      element_mul(e0, Vy, Px);         \
      element_sub(c, c, e0);           \
                                       \
      element_mul(e0, a, QRx);         \
      element_mul(e1, b, QRy);         \
      element_add(e0, e0, e1);         \
      element_add(e0, e0, c);          \
      element_mul(e, e, e0);           \
                                       \
      element_mul(e0, a, Rx);          \
      element_mul(e1, b, Ry);          \
      element_add(e0, e0, e1);         \
      element_add(e0, e0, c);          \
      element_mul(edenom, edenom, e0); \
    }                                  \
  }

  element_set(V, P);
  Vx = curve_x_coord(V);
  Vy = curve_y_coord(V);

  element_set1(v);  // v = 1
  element_set1(vd); // vd = 1

  mpz_init(r);
  mpz_set_ui(r, n);
  i = (mp_bitcnt_t)mpz_sizeinbase(r, 2);
  i = (i > 2 ? i - 2 : 0);

  for (;;) {
    element_square(v, v);   // v = 2v
    element_square(vd, vd); // vd = 2vd
    do_tangent(v, vd);
    element_double(V, V);
    do_vertical(vd, v);

    if (mpz_tstbit(r, i)) {
      do_line(v, vd);
      element_add(V, V, P);
      if (i) {
        do_vertical(vd, v);
      }
    }
    if (!i) break;
    i--;
  }

  element_invert(vd, vd);
  element_mul(res, v, vd);

}

留言

2024-12-03

© 2025 wd-z711

⬆︎TOP