matrix-review-question
矩阵复习题目(划的题+课后题)
划的题
1-4在ipad笔记上。
0x05
考虑上三角矩阵 $\mathbf{A}$
(1)如果 $\mathbf{A}$ 是一个酉矩阵,则 $\mathrm{A}$ 是一个对角矩阵,且对角元素的范数都是 1
(2)如果 $\mathbf{A}$ 是一个上三角 (块) 酉矩阵, $\mathbf{A}=\left(\begin{array}{ll}\mathbf{P} & \mathbf{B} \ \mathbf{0} & \mathbf{Q}\end{array}\right)$,其中 $\mathbf{P}$ 为 $m \times m$ 矩阵,$\mathbf{Q}$ 是 $n \times n$ 矩阵,那么 $\mathbf{P}$ 和 $\mathbf{Q}$ 都是酉矩阵,且 $\mathbf{B}=\mathbf{0}$。
(1)$\mathrm{A}$ 为上三角矩阵,且为酉矩阵 $\Rightarrow \mathrm{A}^H=\mathrm{A}^{-1},\mathrm{~A}^H$ 为下三角矩阵,由于上三角矩阵的逆依旧是上三角阵,因此$A^H$也是上三角矩阵,因此$A^H$必须是对角阵。
(2)$\mathbf{A}$ 为上三角分块酉矩阵, 由 1) 知 $\mathrm{B}=\mathbf{0}$,
且由:
即 $\mathrm{P}$ 和 $\mathrm{Q}$ 均为酉矩阵。
0x06
设 $V_1$ 与 $V_2$ 分别为齐次线性方程组 $x_1+x_2+\ldots+x_n=0$ 和 $x_1=x_2=\ldots=x_n$ 的解空间, 证明 $\mathbb{R}^n=V_1 \oplus V_2$
解:
方程组 $x_1+x_2+\ldots+x_n=0$ 的解空间是 $n-1$ 维的,
方程组 $x_1=x_2=\ldots=x_n$ 的解空间是 1 维的,
由于 $a1, a_2, \ldots, a{n-1}, a$ 线性无关, $V1+V_2=\operatorname{span}\left(a_1, a_2, \ldots, a{n-1}, a\right)=\mathbb{R}^n$ 又因 $\operatorname{dim} V_1+\operatorname{dim} V_2=n-1+1=n$, 根据维数定理:
因此 $\operatorname{dim}\left(V_1 \cap V_2\right)={\boldsymbol{0}}$, 命题成立
0x07
设 $n$ 阶方阵 $\mathbf{A}=\left(a{i j}\right){n \times n}$, 且 $\sum{j=1}^n\left|a{i j}\right|<1, i=1,2, \ldots, n$, 证明 $\mathbf{A}$ 的每一个特征值的绝对值 $|\lambda|<1$
解:
设 $\mathbf{A} \mathbf{x}=\lambda \mathbf{x}, \mathbf{x}=\left(x_1, x_2, \ldots, x_n\right)^T$, 且设 $\left|x_k\right|=\max \left(\left|x_1\right|,\left|x_2\right|, \ldots, \mid x_n\right)$
取 $\mathbf{A x}=\lambda \mathbf{x}$ 的第 $\mathrm{k}$ 个方程:
于是
即有
0x08
证明正规矩阵 $\mathbf{A}$ 若是一个上三角矩阵, 则必是对角矩阵
正规矩阵满足:$\boldsymbol{A}^{\mathrm{H}} \boldsymbol{A}=\boldsymbol{A} \boldsymbol{A}^{\mathrm{H}}$
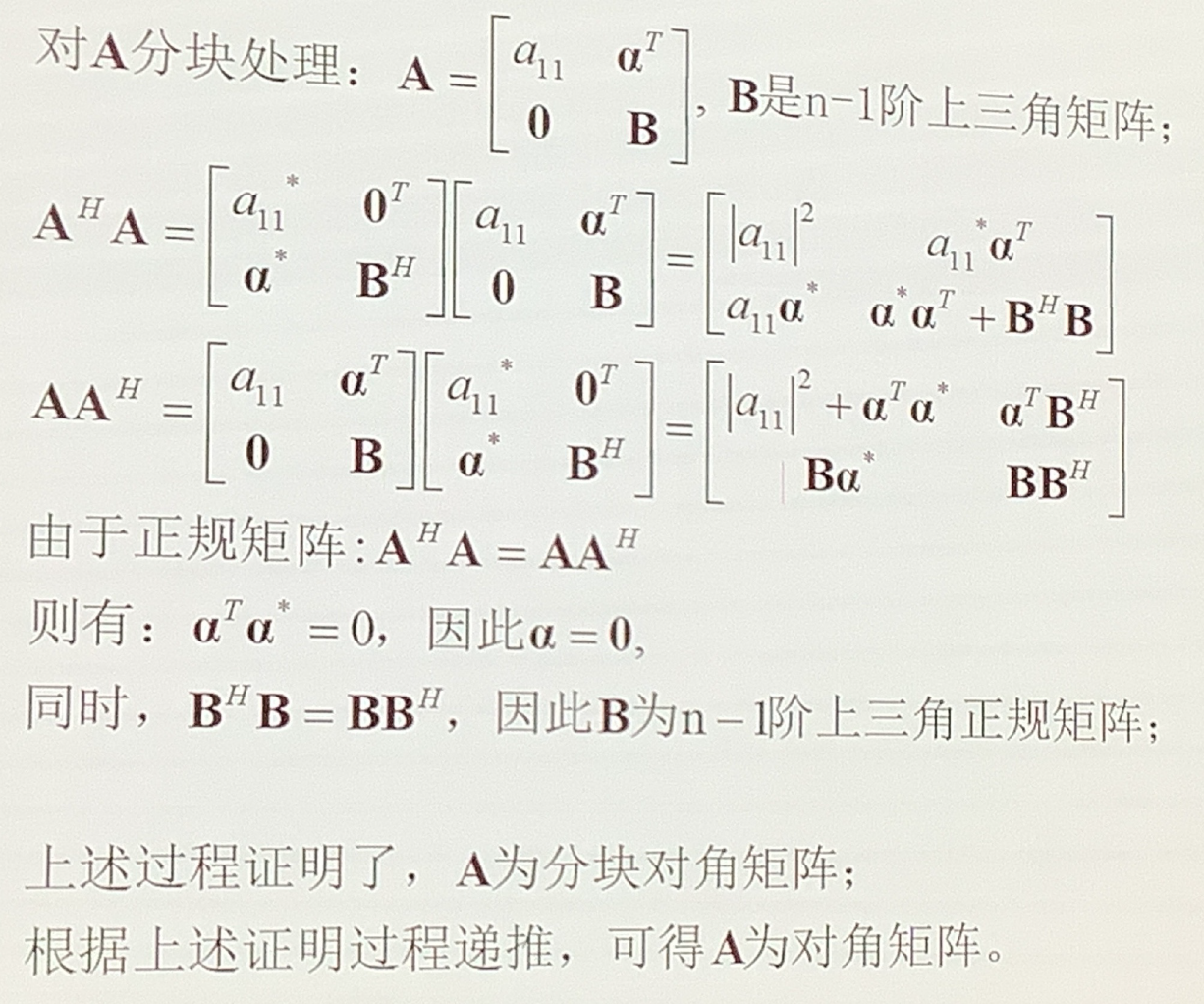
0x09
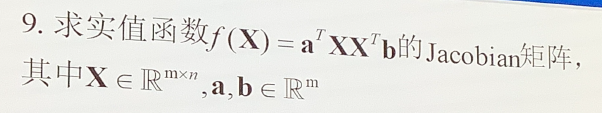
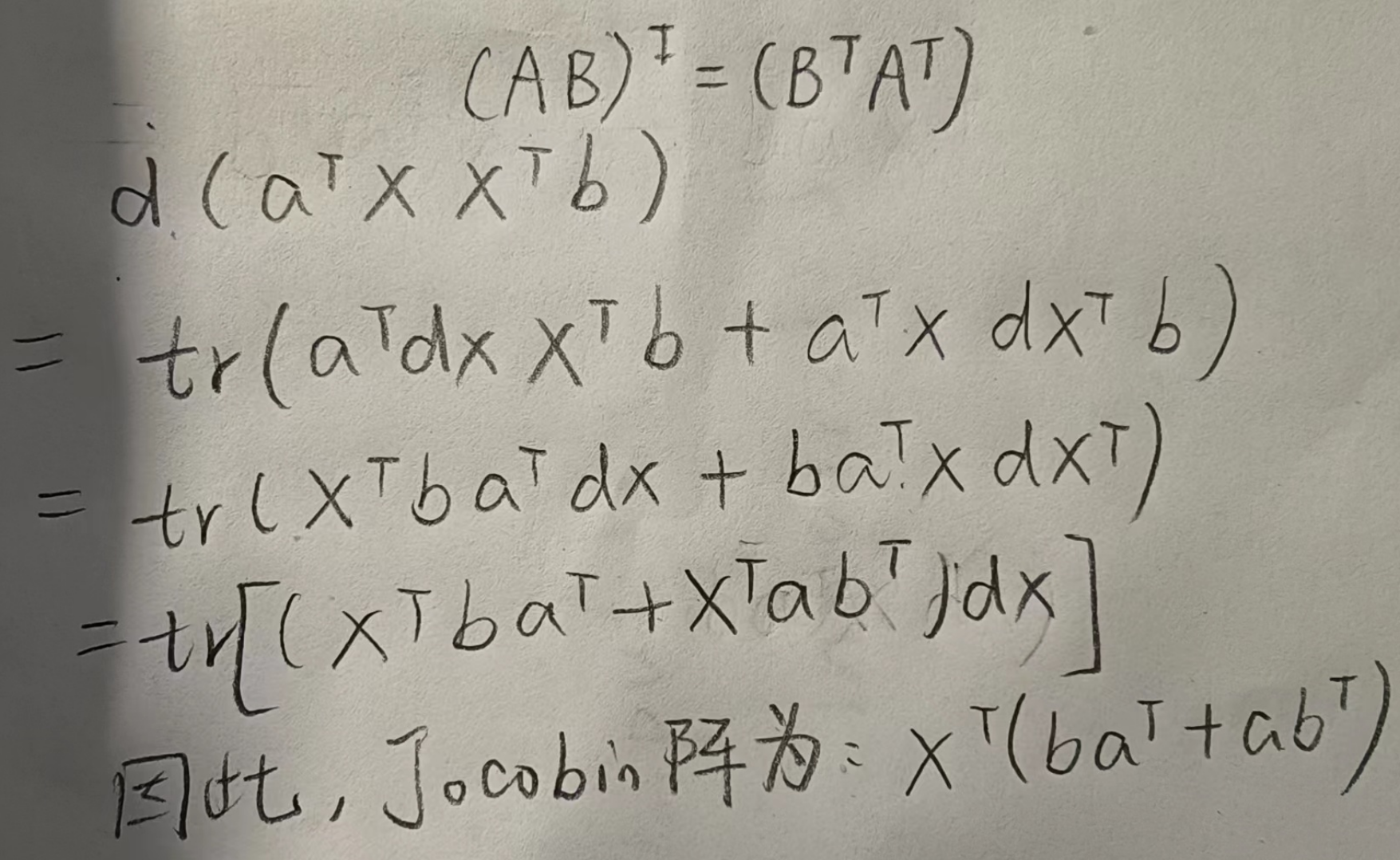
0x10
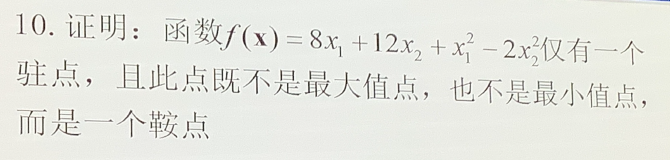

0x11


0x12

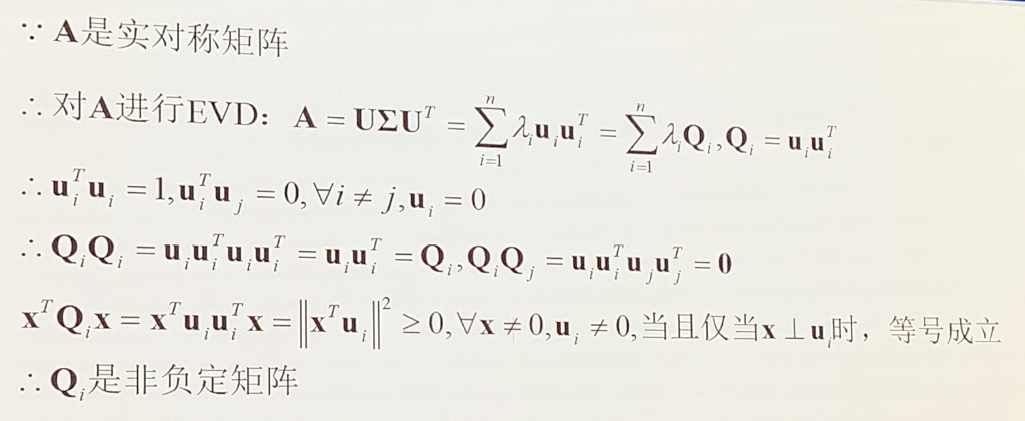
0x14



0x16


0x17



0x18


0x19

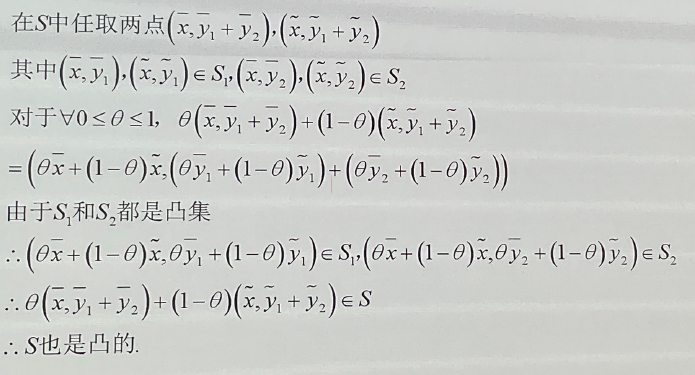
课后题
0x00
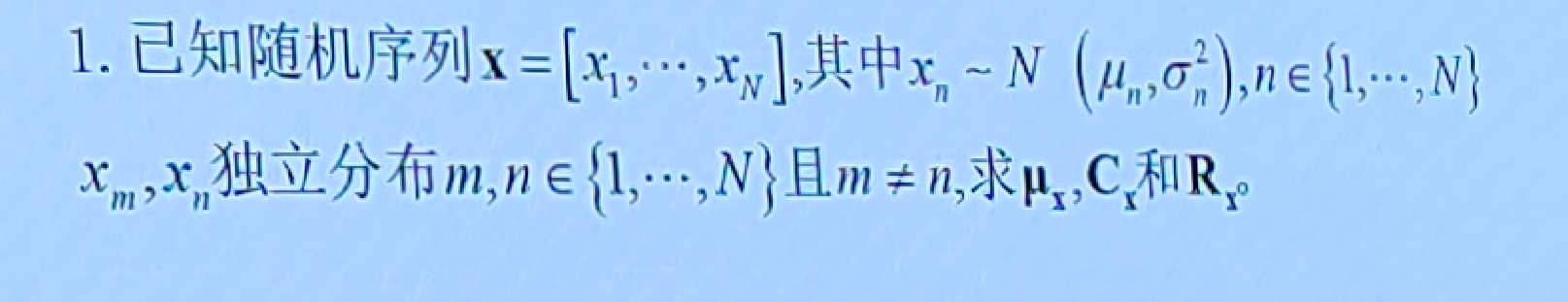

0x01


0x02


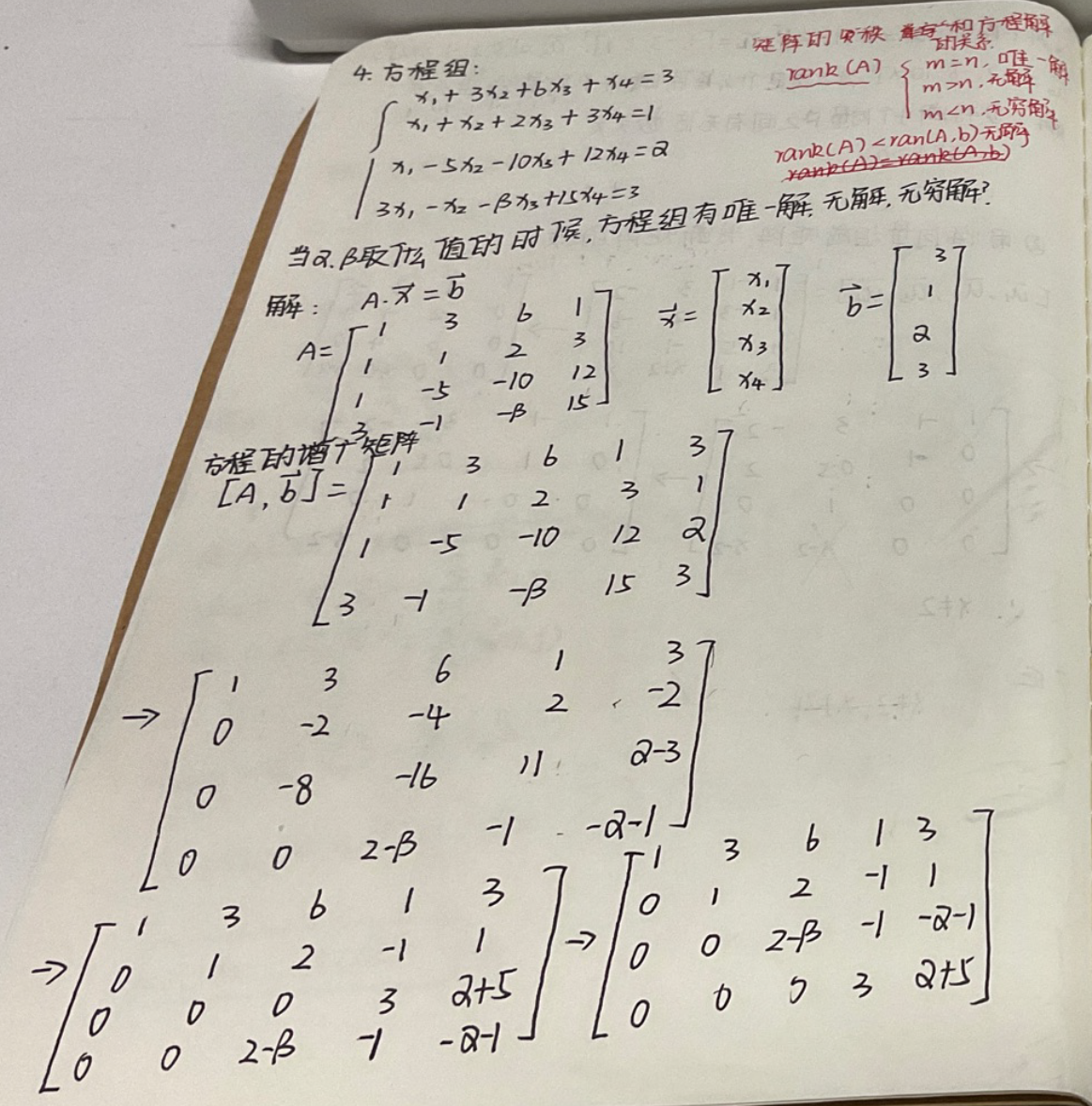




0x03



0x04



0x05


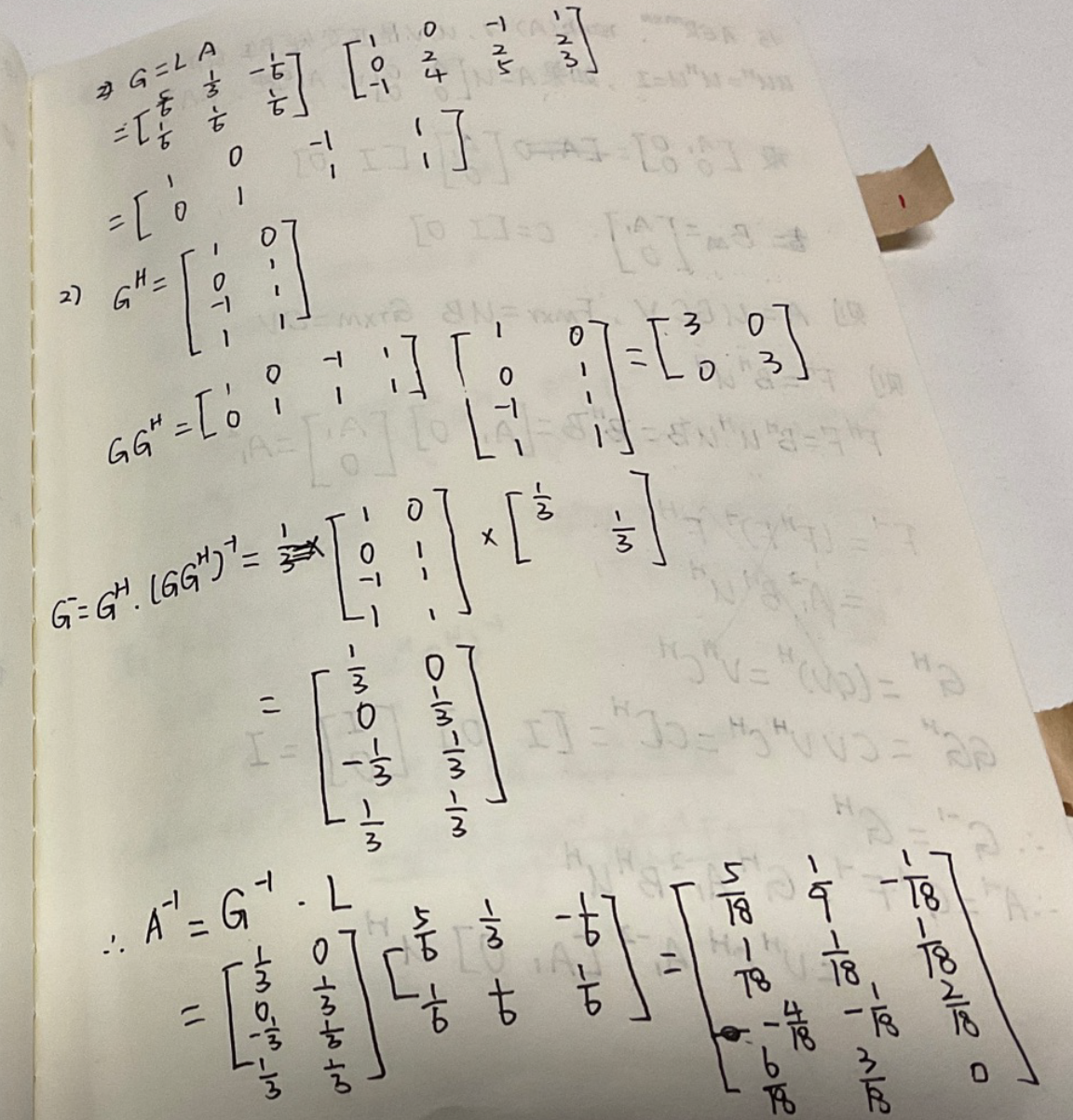
0x06
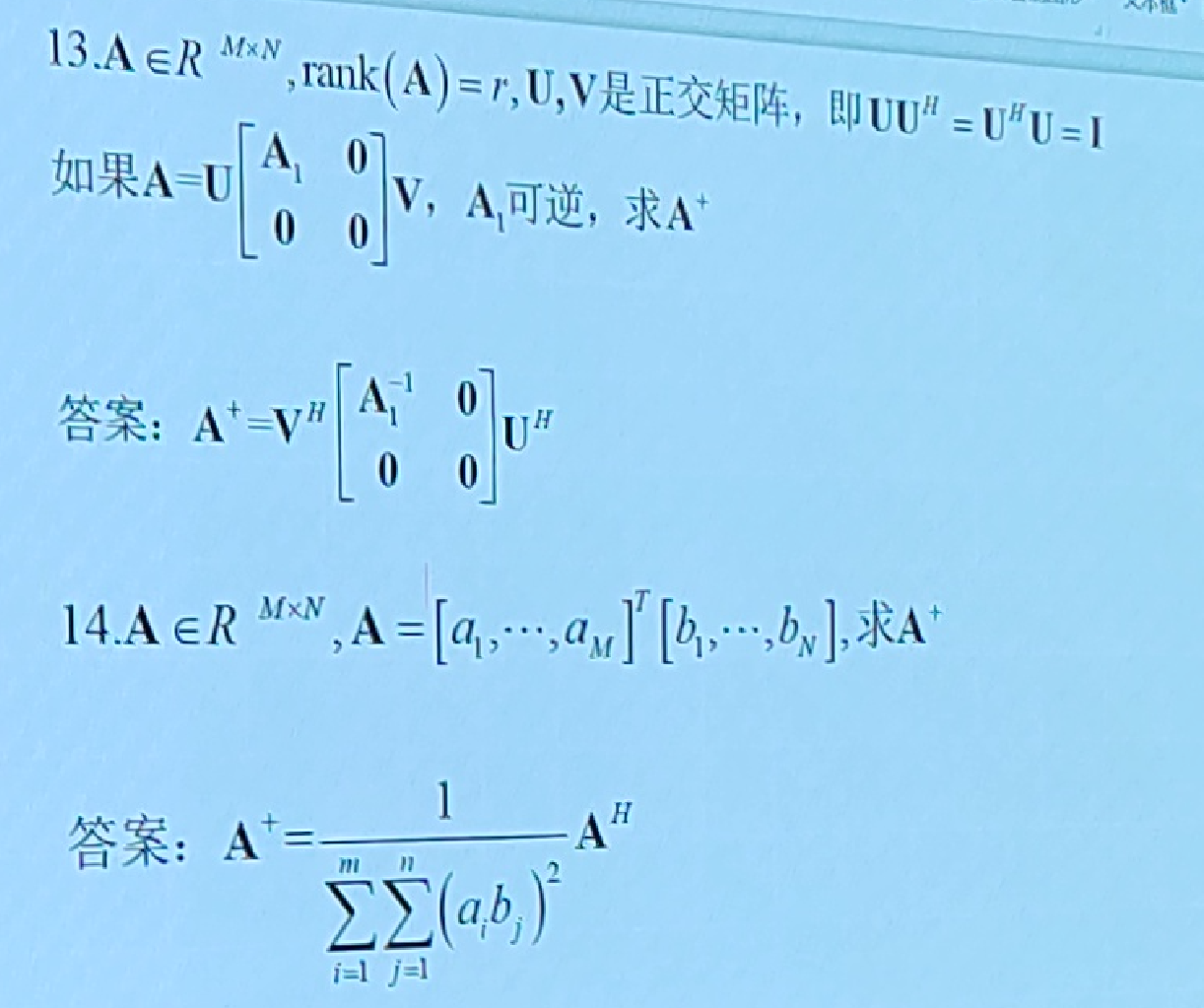
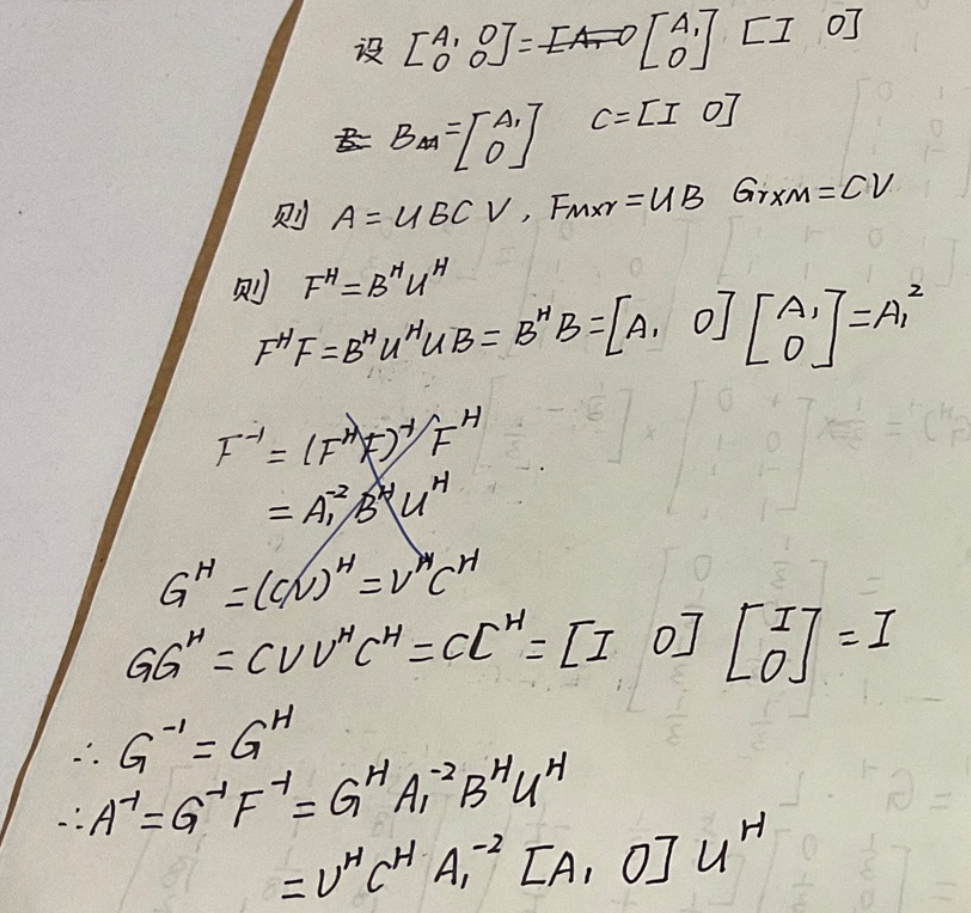



0x07



0x08


0x09


0x10




0x11

0x12


0x13
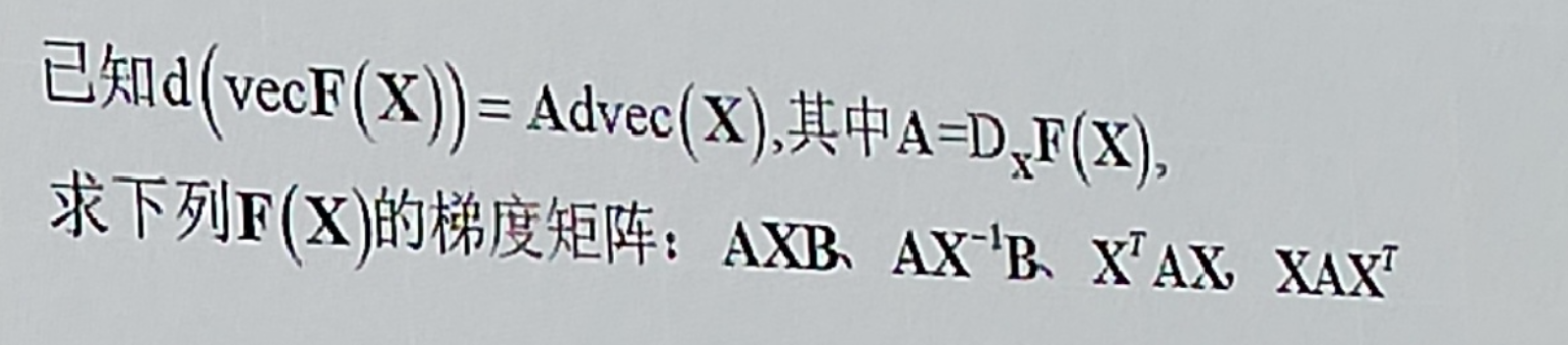

0x15

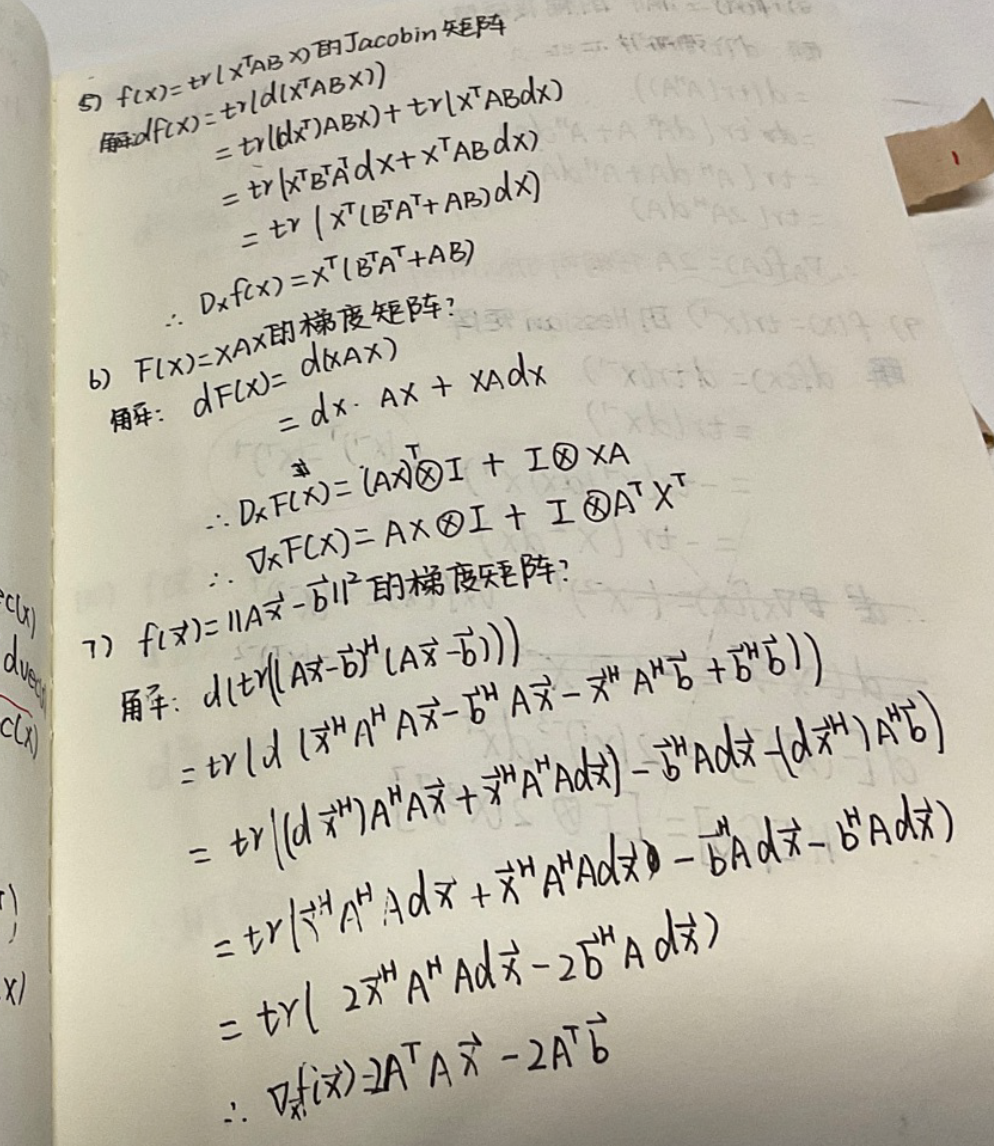


0x16

0x17
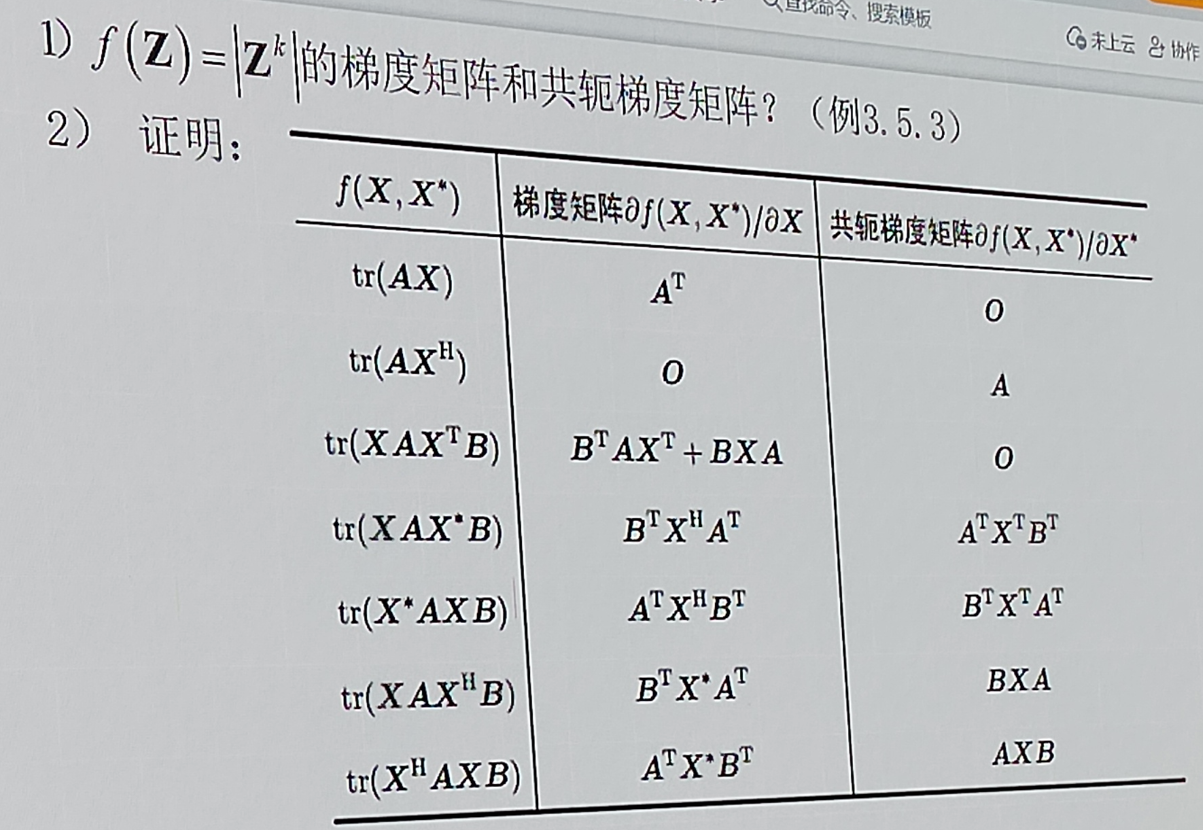


0x18




0x19

0x20

0x21

0x22
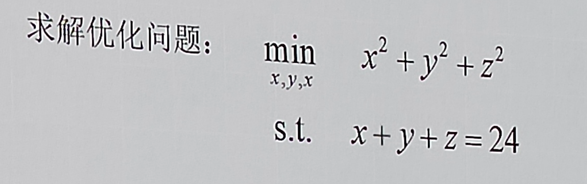

0x23


0x24


0x25


0x26


0x27

0x28
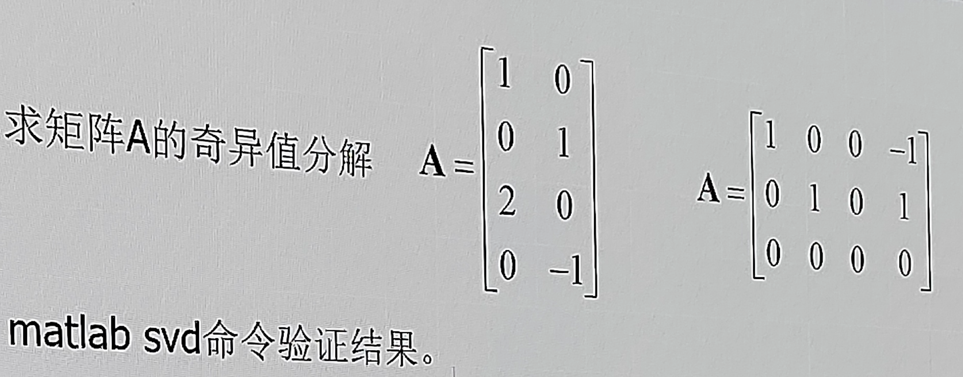

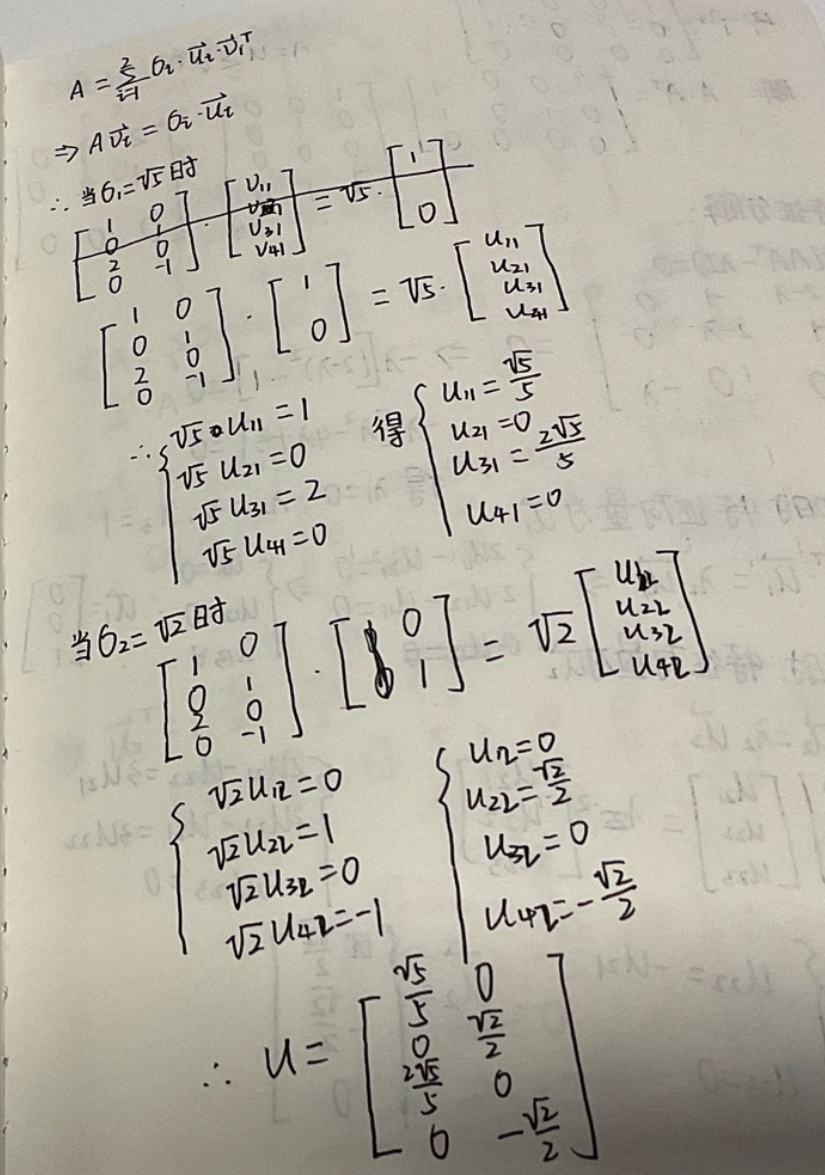



0x29
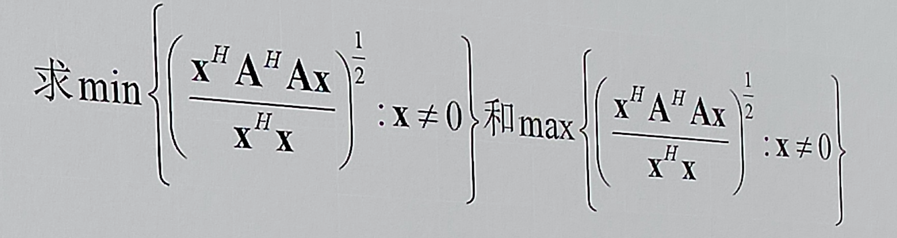
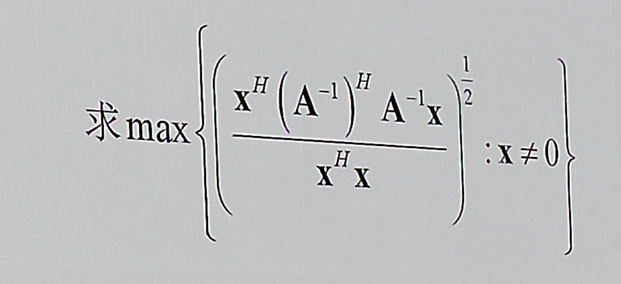

0x31





0x33




0x35


0x36


0x37
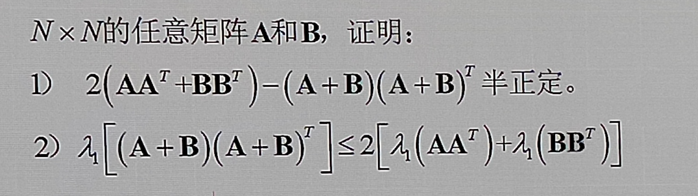




0x39



0x40


0x41



0x43


0x44

0x45

0x46


留言
- 文章链接: https://wd-2711.tech/
- 版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 许可协议。转载请注明出处!