矩阵分析与应用笔记

0x00 矩阵的基本概念

• 向量空间。以向量为元素的集合，N维向量的集合称为N维空间。

• 子空间。子空间是向量空间的子空间，满足：（1）加法闭合性。（2）乘法闭合性。（3）包含0向量。

• 各种矩阵：

• 常数向量：$a=[1,5,4]^T$；函数向量：x=[1,x^2,x^3]^T；随机向量（向量的元素是随机变量）：x(n)=[x_1(n),x_2(n),x_3(n)]^T。其内积分别为：

• 范数（距离），如下所示：

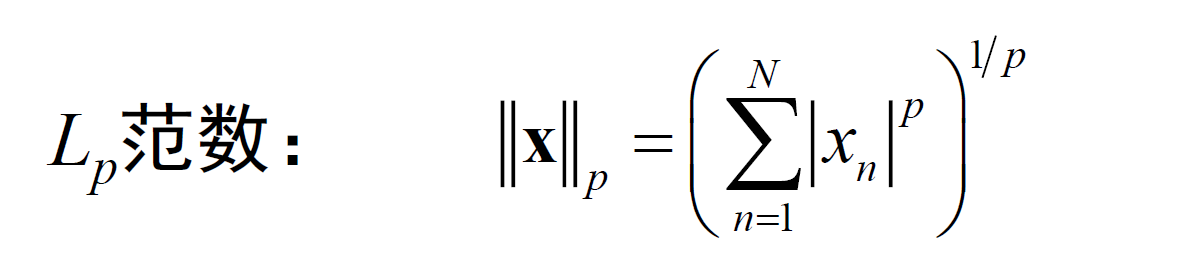
 其性质如下：

• 向量夹角计算如下：

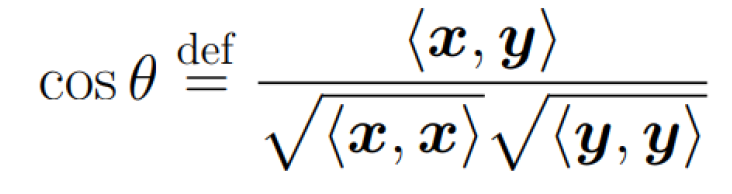
• 正交。内积等于零，对常数向量和函数向量；或者它们的外积的数学期望等于零矩阵，对随机向量。

• 累积分布函数F[x(t)]与概率密度函数f[x(t)]。

• 自相关矩阵R_x。CN(0,1)表示均值为0，实虚部统计独立且方差各为1/2的复高斯分布。i.i.d指的是独立同分布。

• 自协方差矩阵C_x。关系为：C_x=R_x-\mul_x\mul_x^H

• 也存在互相关矩阵与互协方差矩阵，两者关系也如上述所示。
• 相关系数。c_{xy}是两个随机变量之间的互协方差。

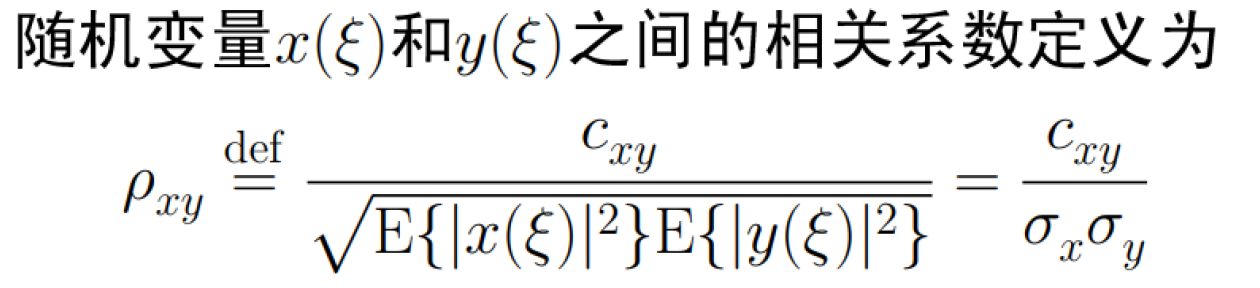
 当\rho_{xy}=0时，那么两个随机变量统计不相关。若两个随机向量正交，那他们的互相关矩阵为零矩阵。

• 高斯随机向量。

• KNN的原理：（1）计算待分类点到每个样本点间的距离。（2）对每个距离进行排序，选择出距离最小的K个点。（3）将待分类点归入在K个点中占比最高的那一类。

• Euclidean距离的缺点：不同属性等同看待。而Mahalanobis距离是一种度量数据之间相似度的指标，它考虑了数据的协方差结构，可以修正Euclidean距离中各个维度尺度不一致且相关的问题，其公式为：

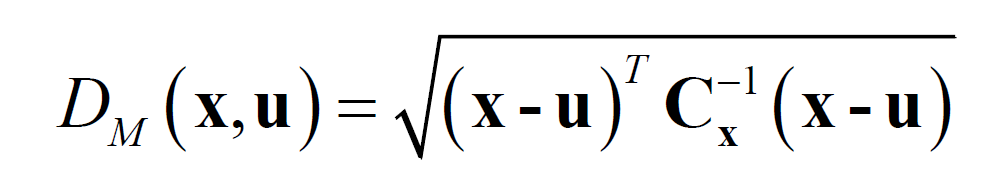
 Mahalanobis距离使用协方差结构可以修正维度尺度不一致且相关的问题，因为协方差矩阵可以反映数据的各个维度之间的相关性和尺度差异。如果数据在某个维度上有较大的方差，那么该维度对应的协方差矩阵元素会较大，从而使得该维度对应的马氏距离缩小；反之，如果数据在某个维度上有较小的方差，那么该维度对应的协方差矩阵元素会较小，从而使得该维度对应的马氏距离放大。这样就可以消除不同尺度带来的影响。另外，如果数据在不同维度之间有较强的相关性，那么协方差矩阵会有较大的非对角元素，从而使得马氏距离考虑到了数据在不同维度上投影后产生的偏移。这样就可以消除相关性带来的影响。

• 线性无关&非奇异矩阵。奇异矩阵的定义是行列式等于0的方阵，非奇异矩阵的定义是行列式不等于0的方阵。

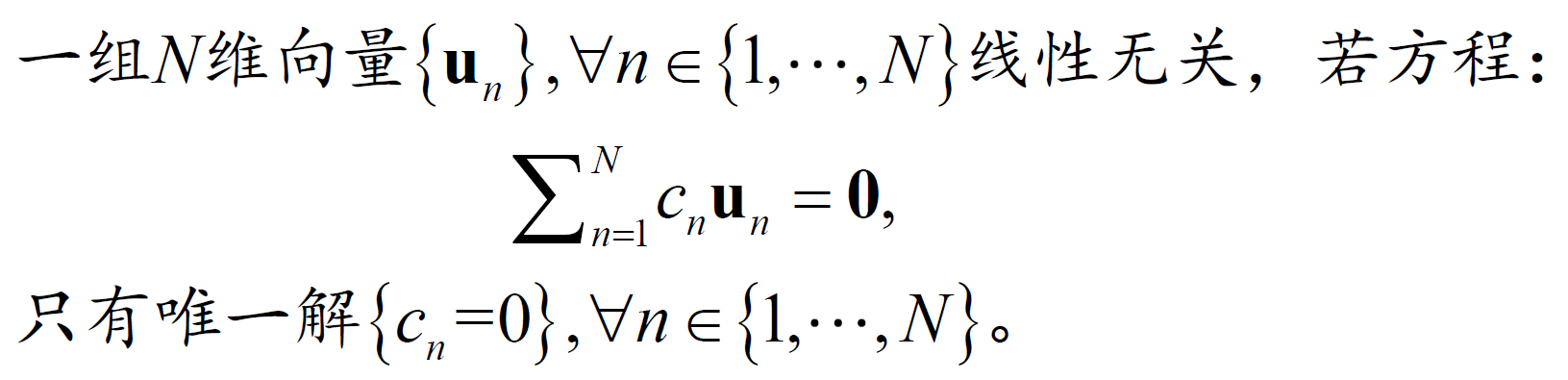
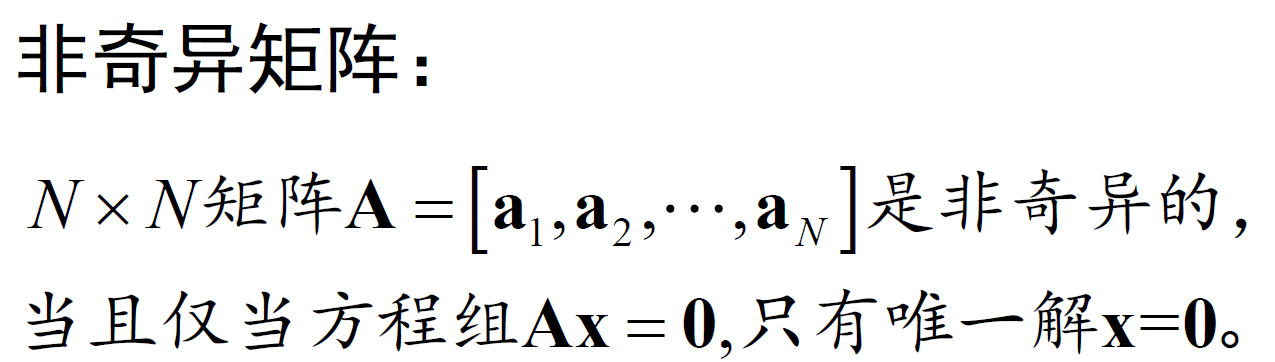
• 矩阵的L_p范数与Frobenius范数，以及矩阵范数的性质：

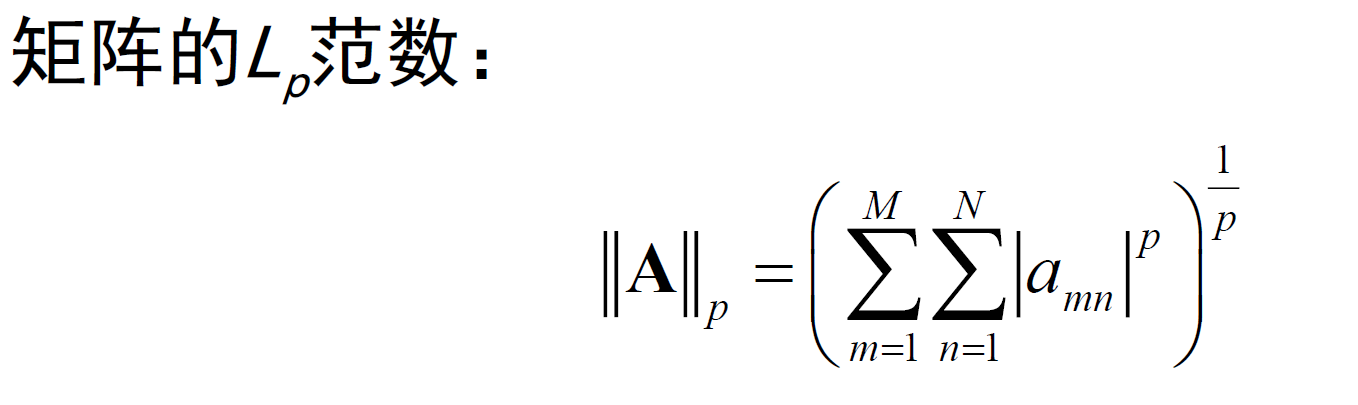
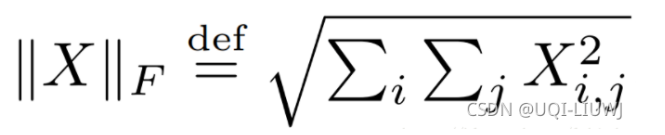
 注：矩阵对角元素之和叫做矩阵的迹，符号为tr(A)。

• 矩阵A与B的内积如下：

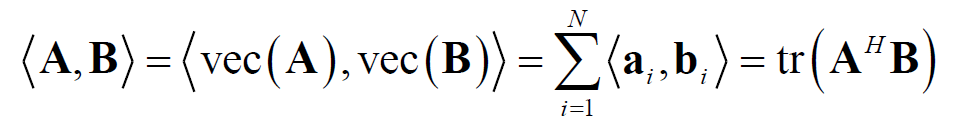
• 矩阵内积与范数之间的关系如下：

• 二次型与正定。

• 行列式。其中A_{ij}是删掉第i行第j列后剩下的矩阵。

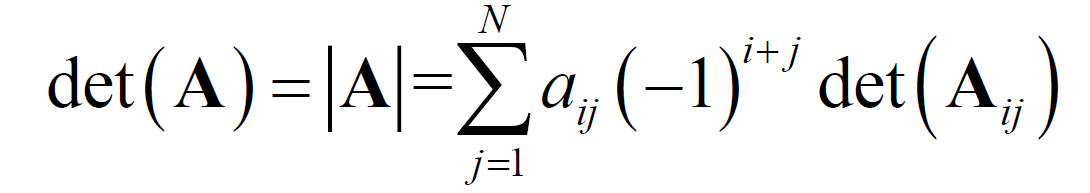
• 特征值与特征向量。

 且特征值满足：

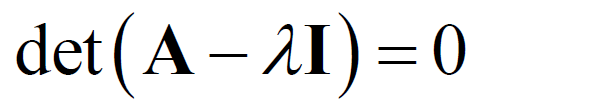
 如果有一个特征值为0，那么A就是奇异矩阵。正定矩阵就是特征值全是正实数的矩阵。

• 矩阵的迹。

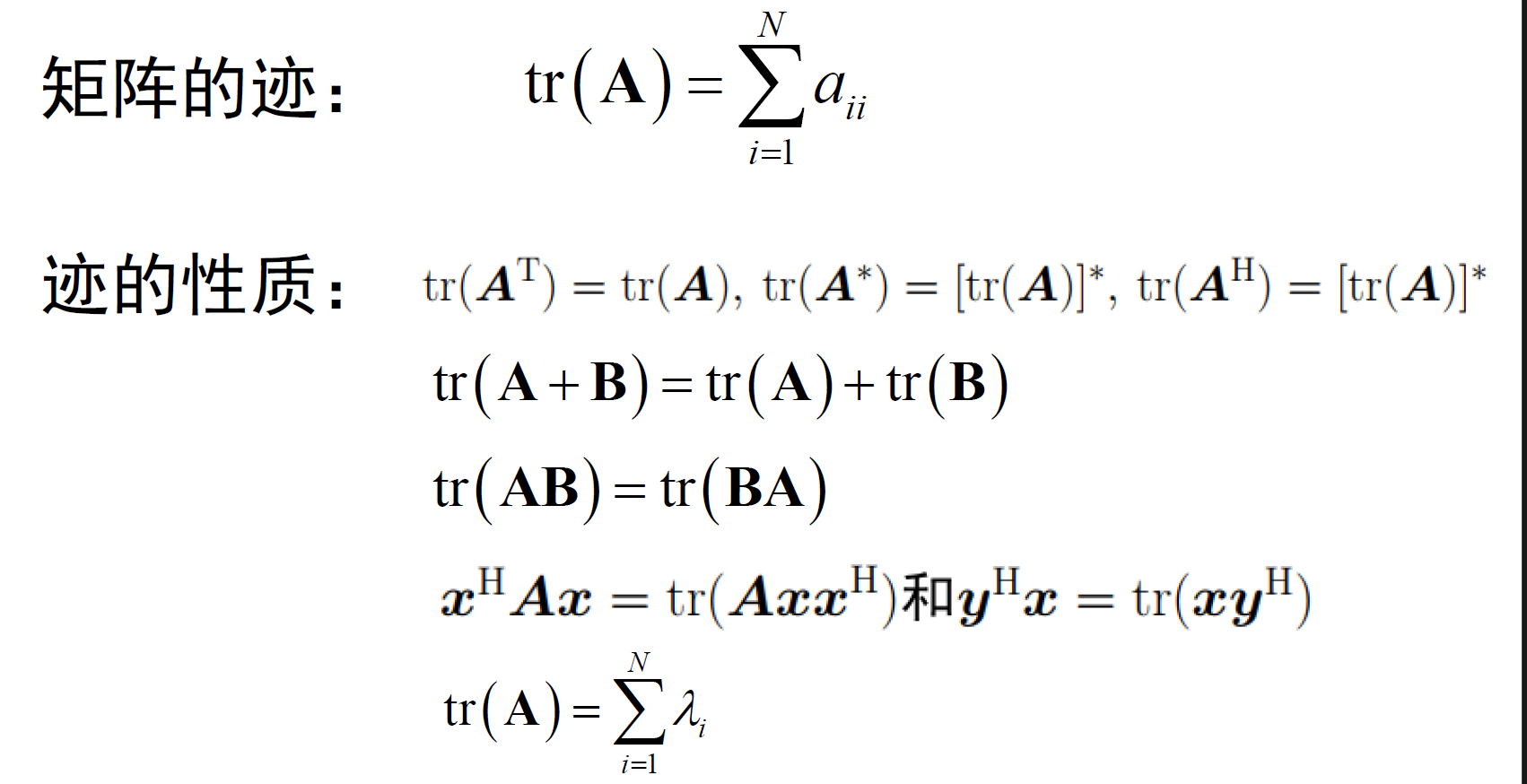
• 矩阵的秩。矩阵A中线性无关行的数目。

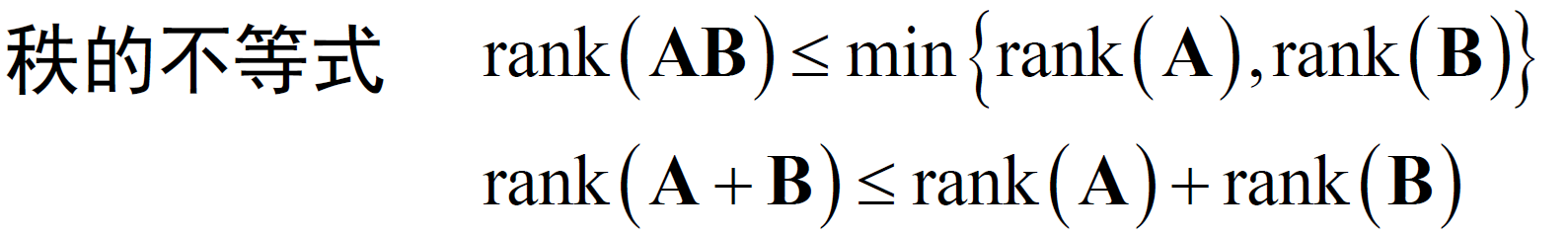
• 适定/欠定/超定方程。

• 矩阵的逆。下列是矩阵有逆的充要条件：

 矩阵逆的性质有：

 知识补充：

1
2

1. 正交矩阵：正交矩阵是一个方块矩阵，其元素为实数，且行向量与列向量皆为正交的单位向量， A^T = A^{-1}
2. 酉矩阵：酉矩阵是一种复数方阵，它的共轭转置（即把每个元素取共轭再转置）等于它的逆矩阵，可以看作正交矩阵在复数域的推广

• 分块矩阵的逆：

 因此有：

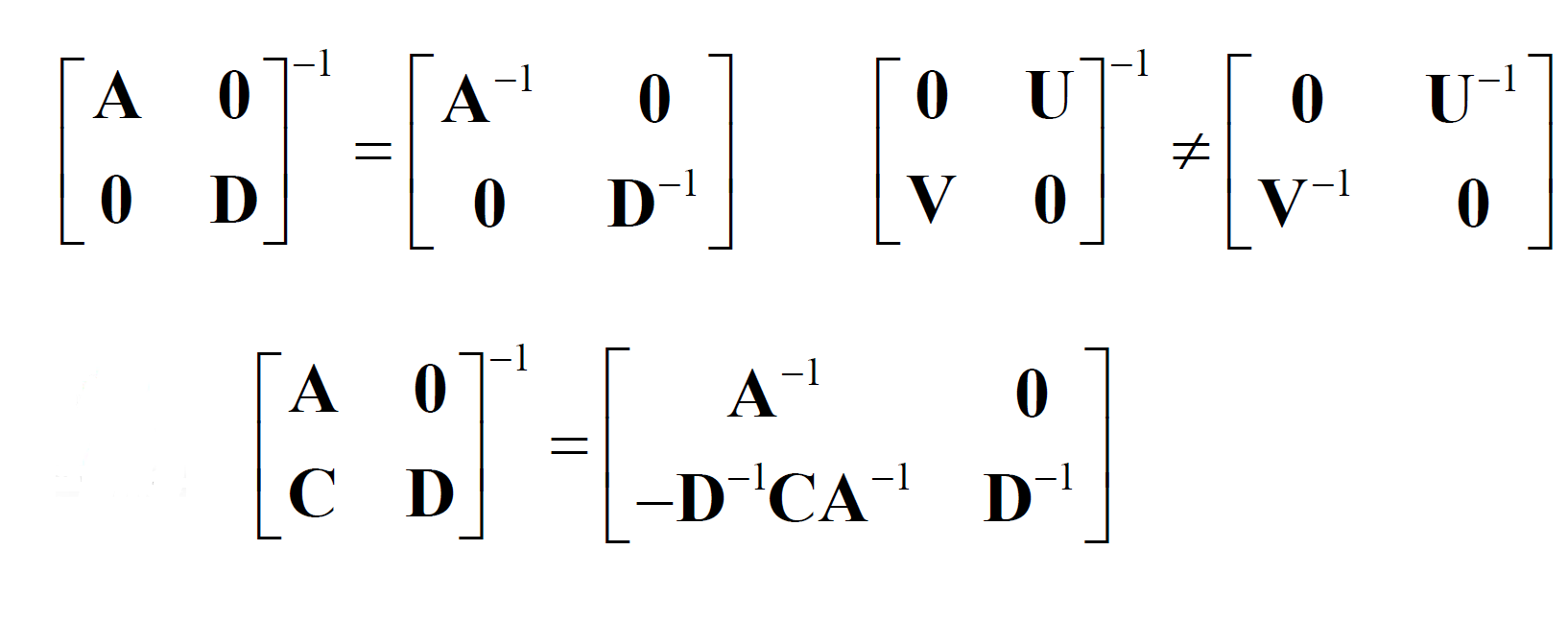
• Hermitian矩阵的逆：

• 左逆矩阵&右逆矩阵

• 左伪逆矩阵&右伪逆矩阵

• 广义逆矩阵（有缺陷）

• 如果G是A的广义逆矩阵（A的形状为m*n），那么G要满足以下条件：

• 如何求广义逆矩阵，也叫Moore-Penrose逆矩阵：

• Kronecker积

• Hardmard积与直和

 Hardmard积的性质如下：

课后习题：

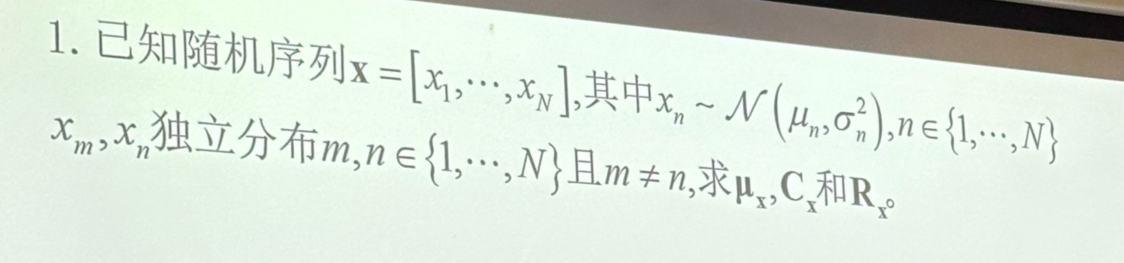
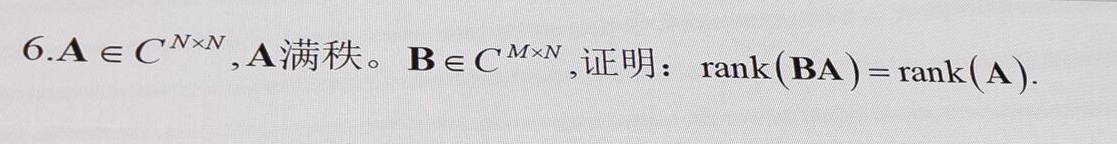
0x01 特殊矩阵

• 基本矩阵

• 移位矩阵，通过左乘或右乘，将矩阵的行列顺序反转

• 选择矩阵

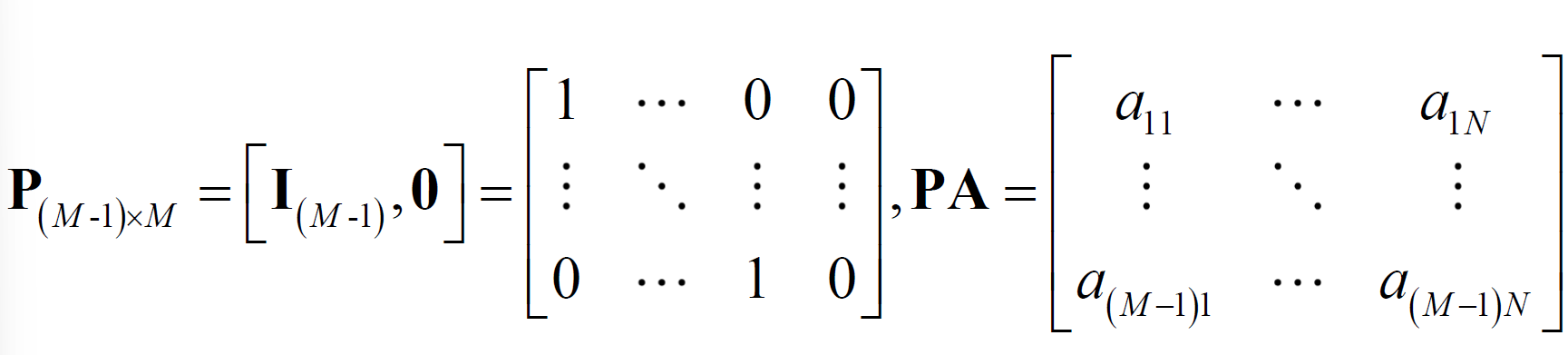
• 置换矩阵

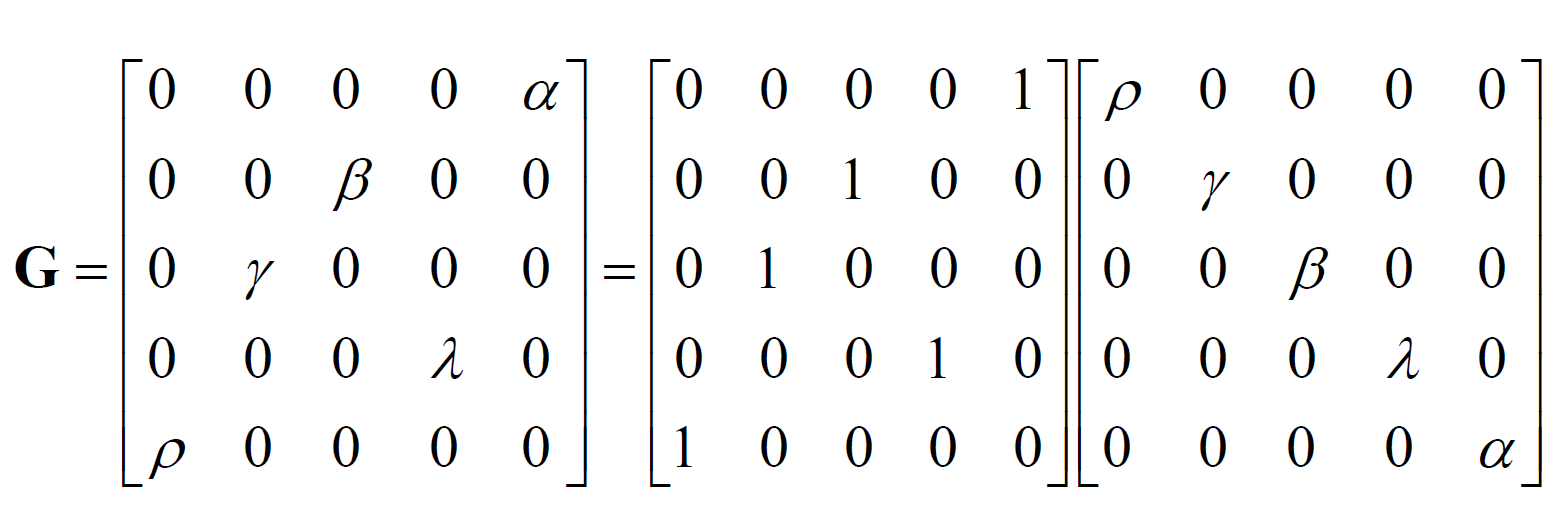
• 正交矩阵与酉矩阵

• 酉变换与正规矩阵

• 实向量、实矩阵与复向量、复矩阵的比较

• 中心化矩阵

• 相似矩阵

 证明如下：（主要是行列式的性质与迹的性质）。补充：例如A有特征值\lambda，那么A的特征多项式为|det(A-\lambda*I)|。

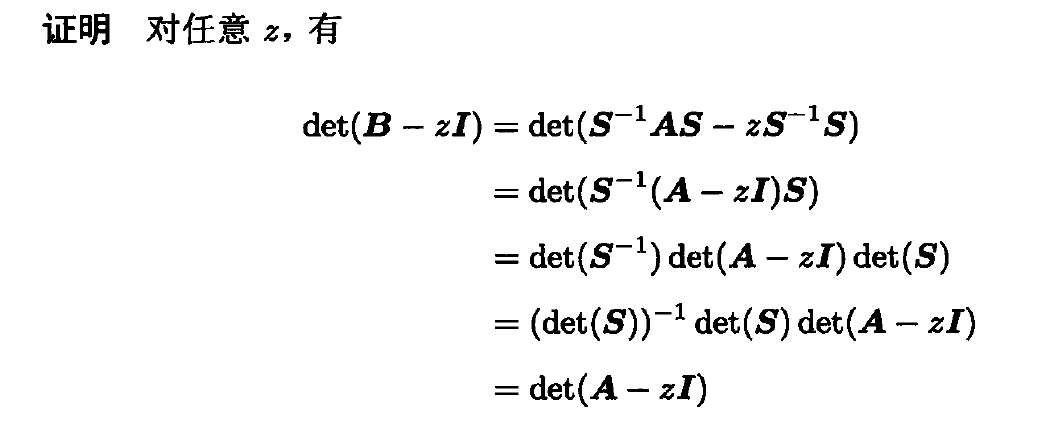
 相似矩阵的性质：

• 相合矩阵

• 三角矩阵

 补充：hermitian矩阵：共轭转置与自己相等。

• Vandermonde矩阵

 信号的DFT：信号的离散傅里叶变换，将时域上的离散信号变为频域上的离散信号。

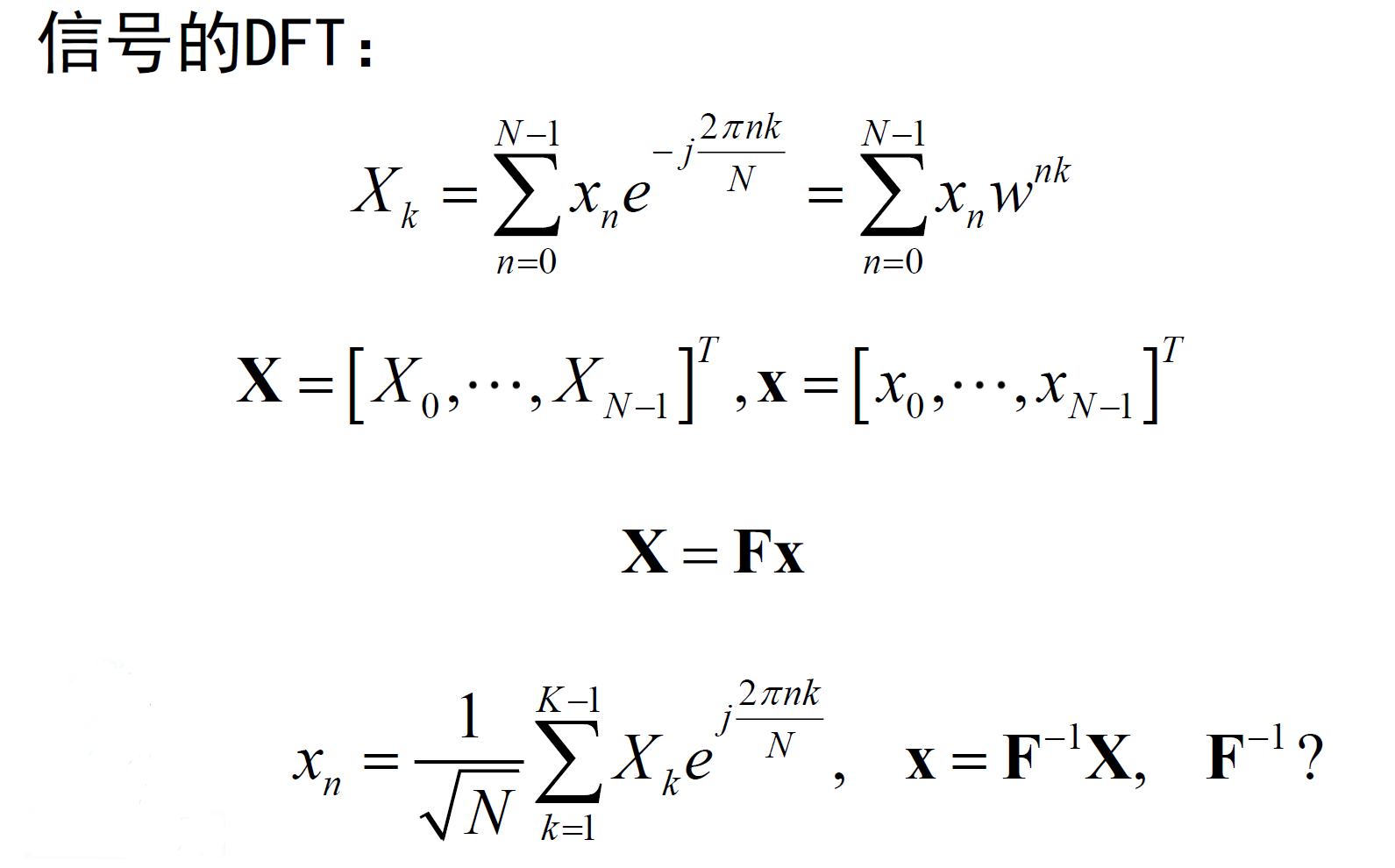
• Fourier（傅里叶）矩阵

• Hadamard矩阵

• Toeplitz矩阵：对角线元素取相同值

0x02 矩阵的微分

• 矩阵函数

 借助e^x的泰勒级数展开。

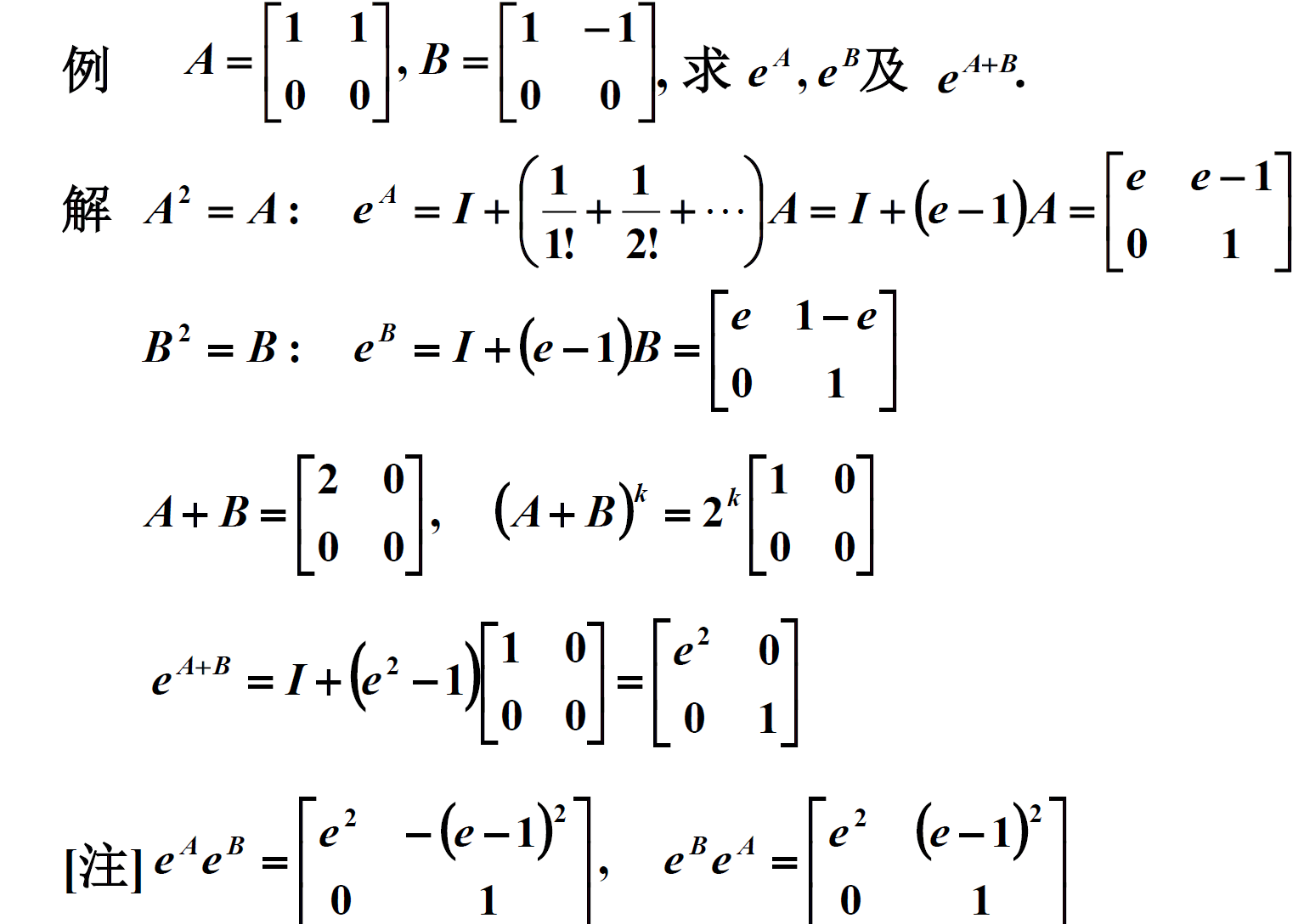
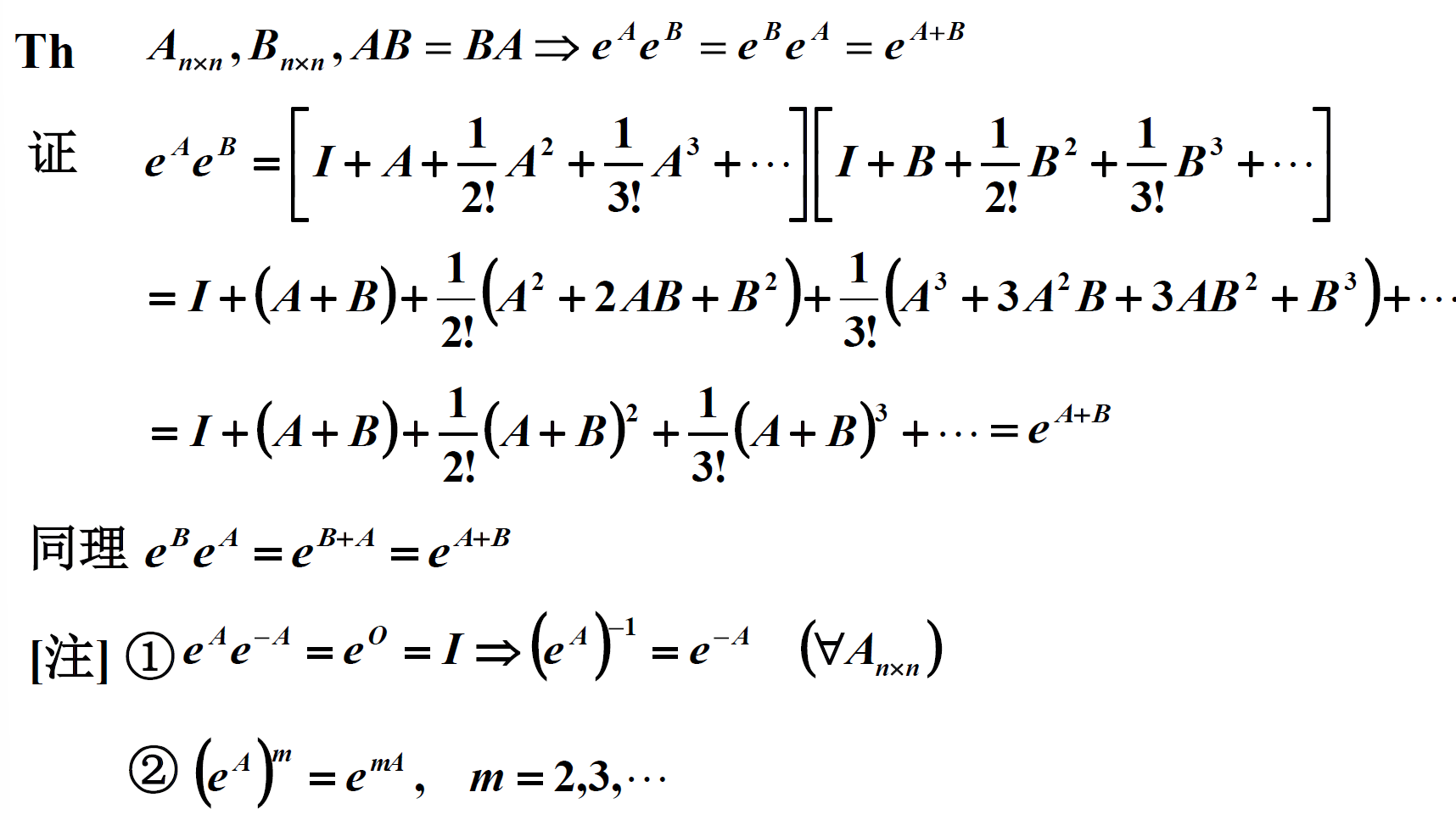
 利用欧拉公式e^(iz)=cosz+i*sinz，有：

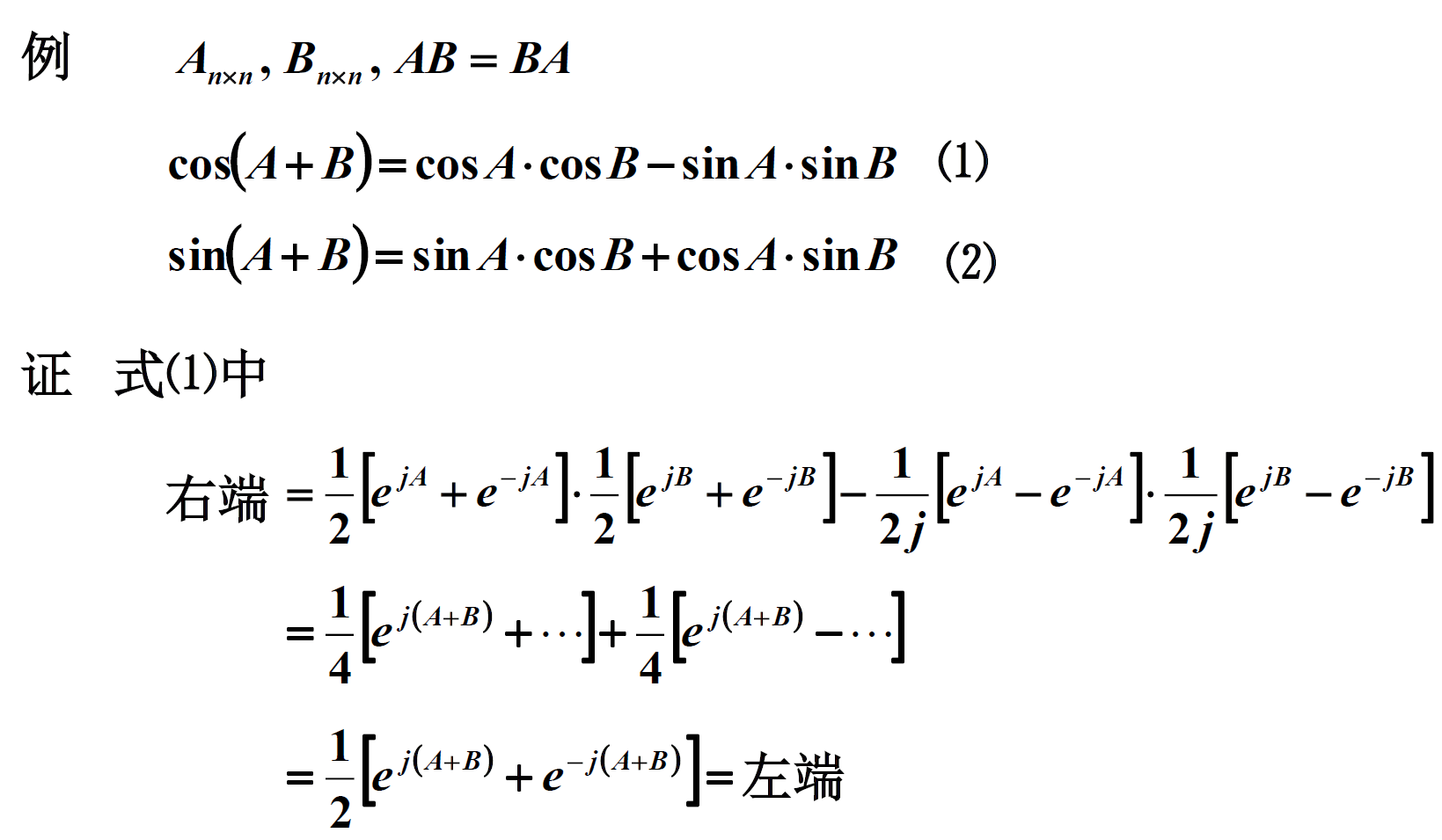
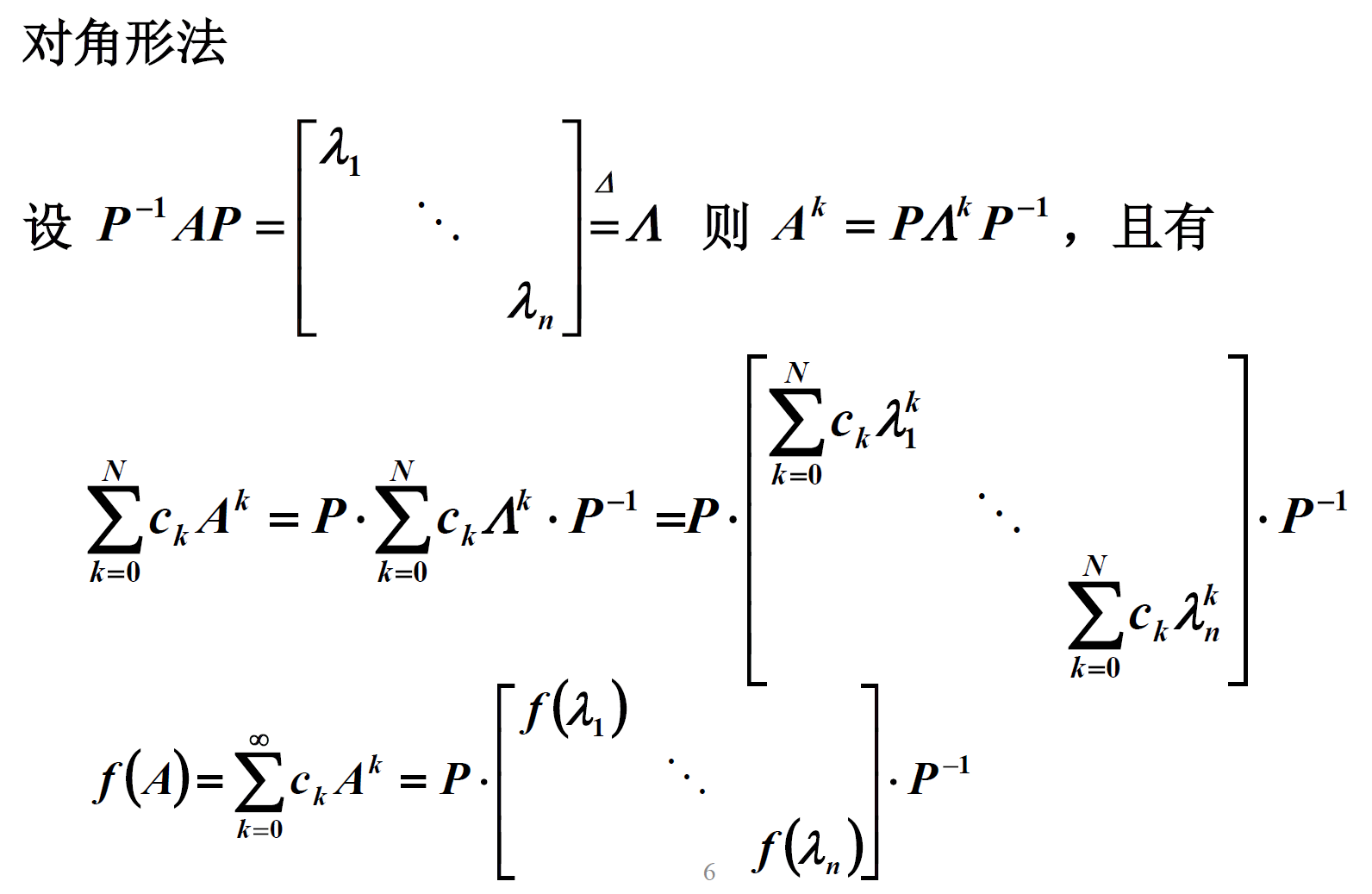
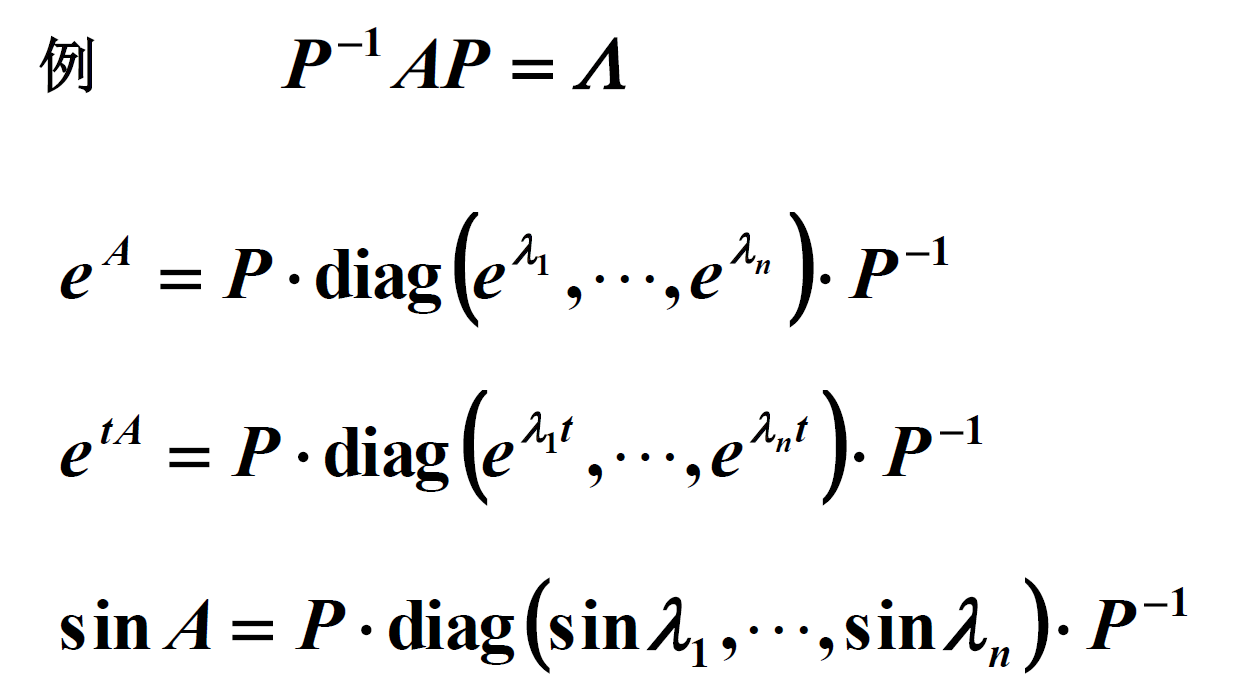
• 矩阵微分

  • 函数分类

  

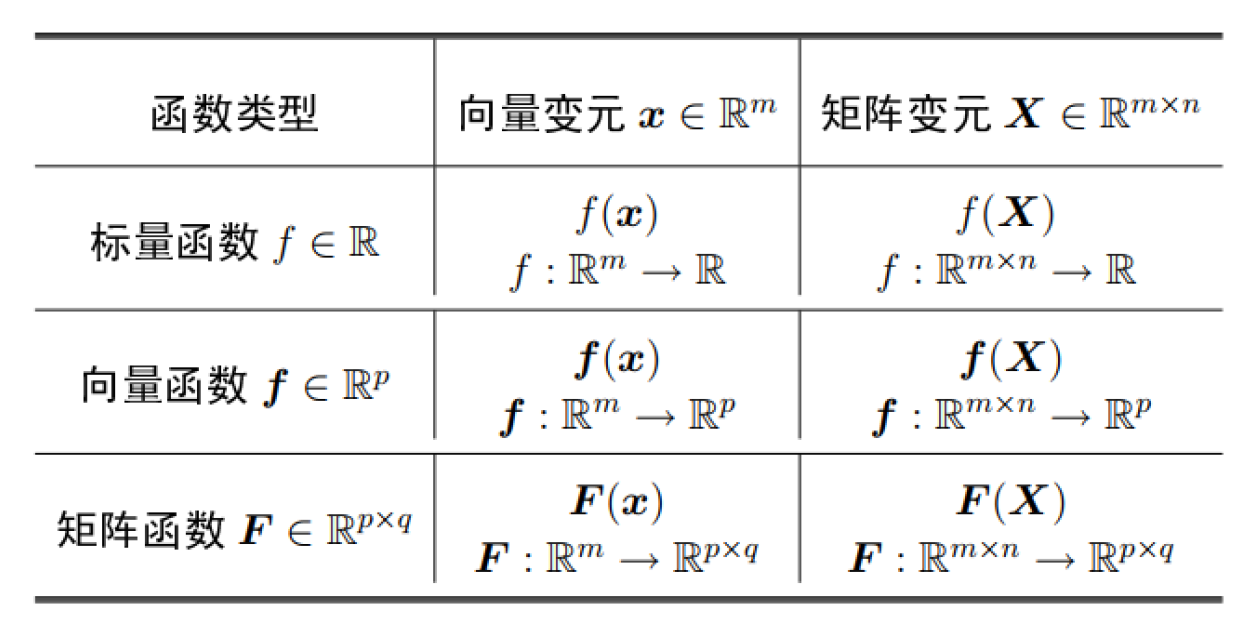
  • 标量函数的行向量求偏导

  

  

  • 标量函数的列向量求偏导

    

  • 标量函数的梯度流

  

  • 向量函数的协梯度矩阵

  

  • 矩阵函数的协梯度矩阵

  

  

  • 例子：（Jacobian矩阵：雅可比矩阵是一阶偏导数以一定方式排列成的矩阵）

  

  

  

  

• 标量函数的微分

• 微分与梯度矩阵（求f(X)梯度矩阵的方法）

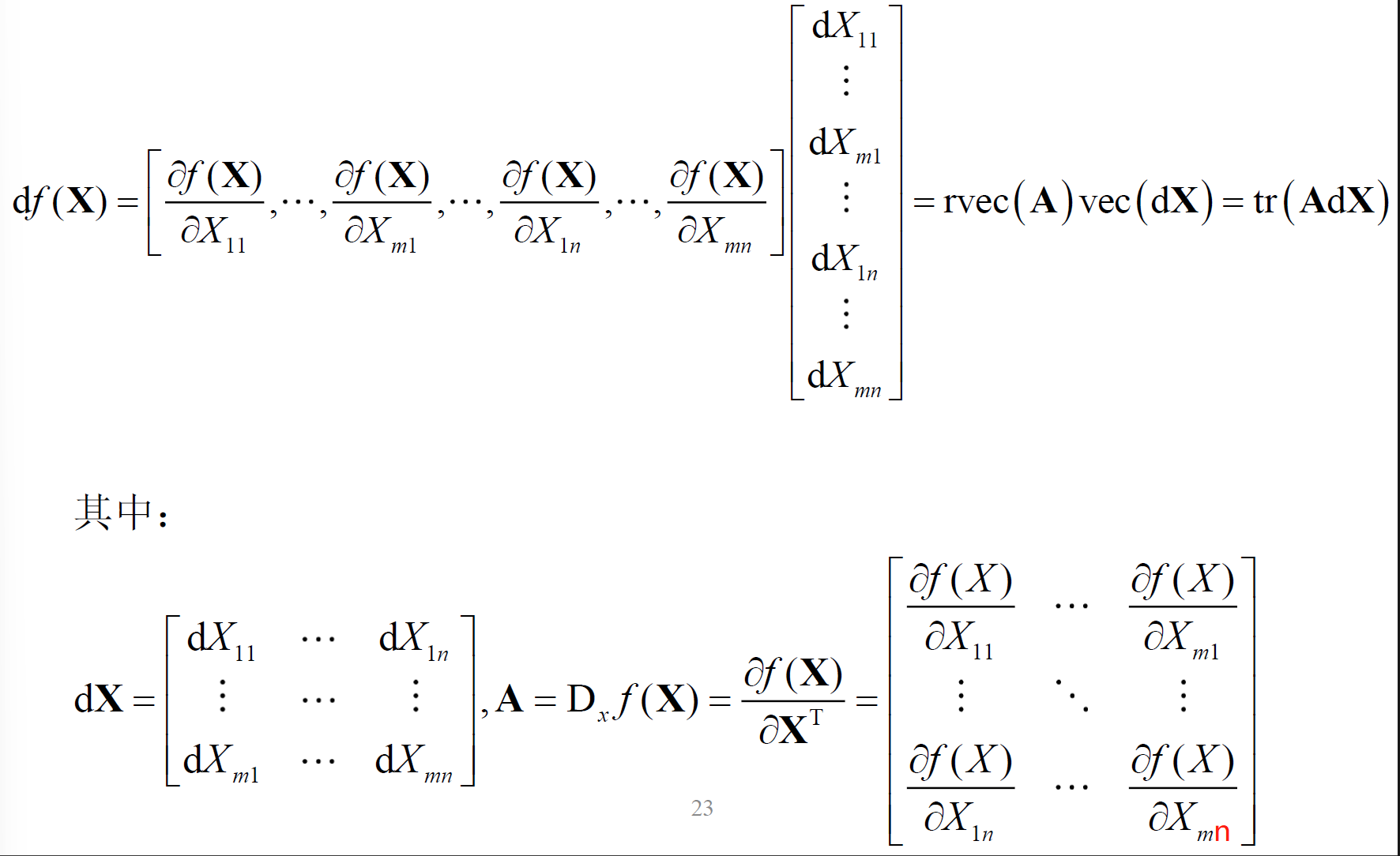
• 实标量函数的微分计算

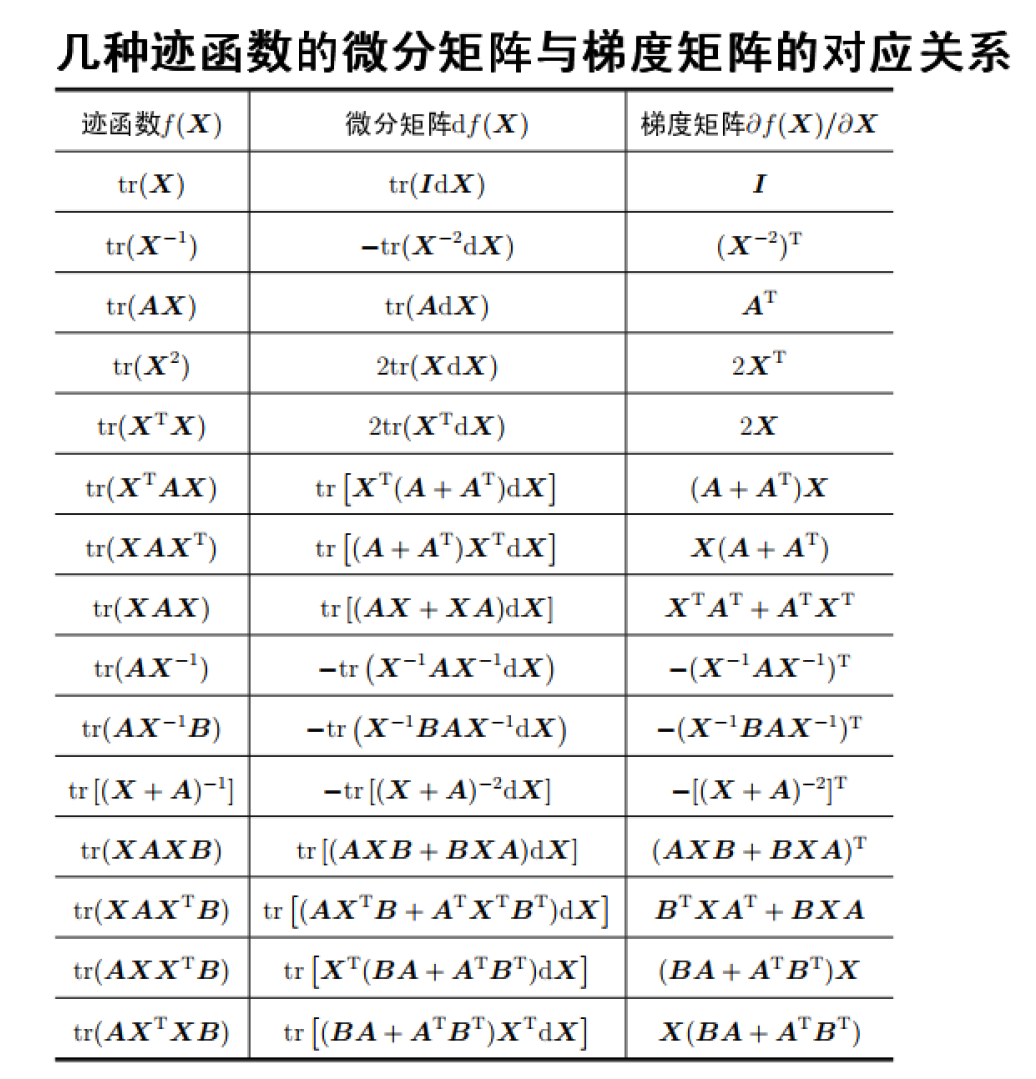
• 矩阵微分常用公式

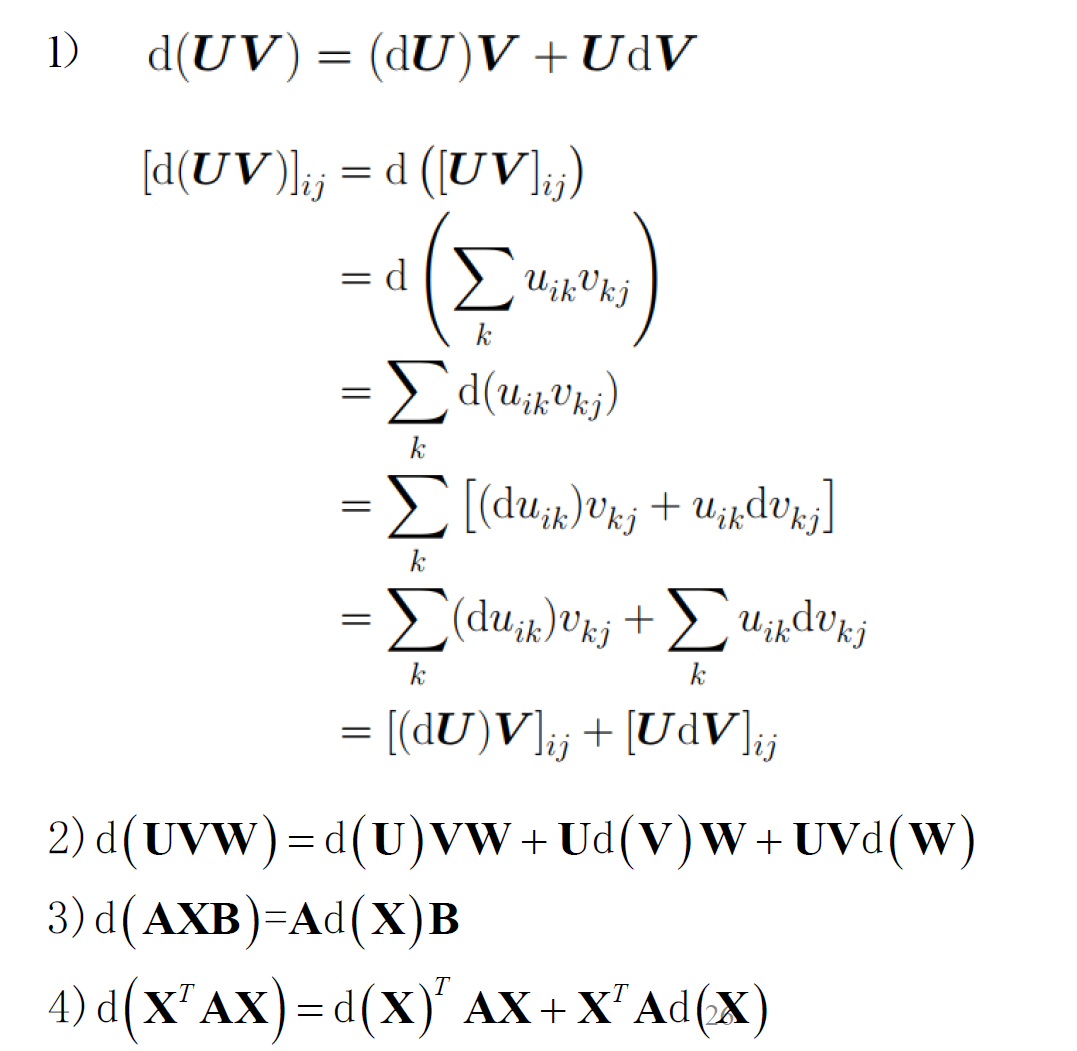
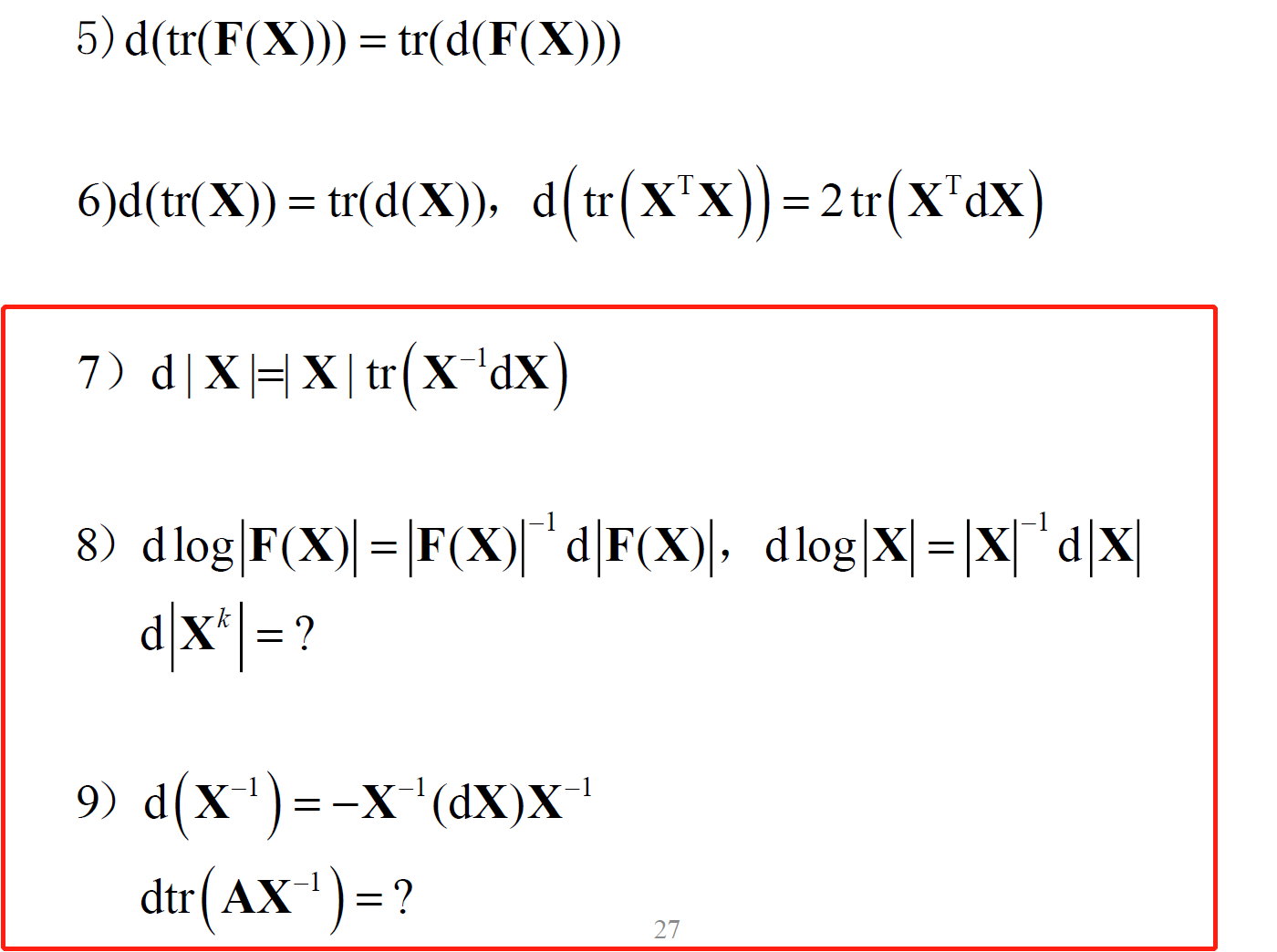
 上面几条性质都挺难的，没证明出来。。

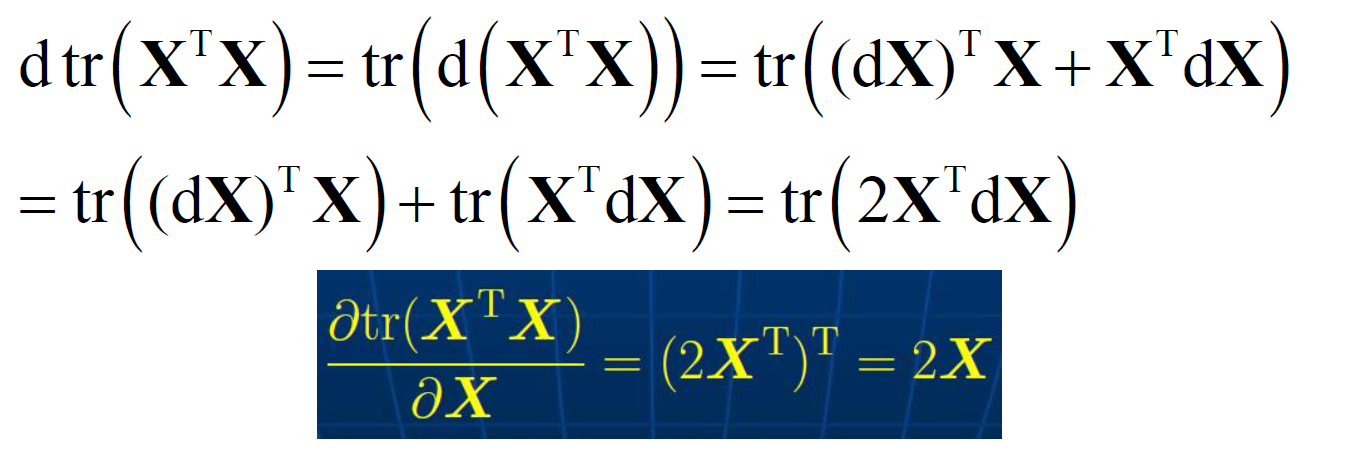
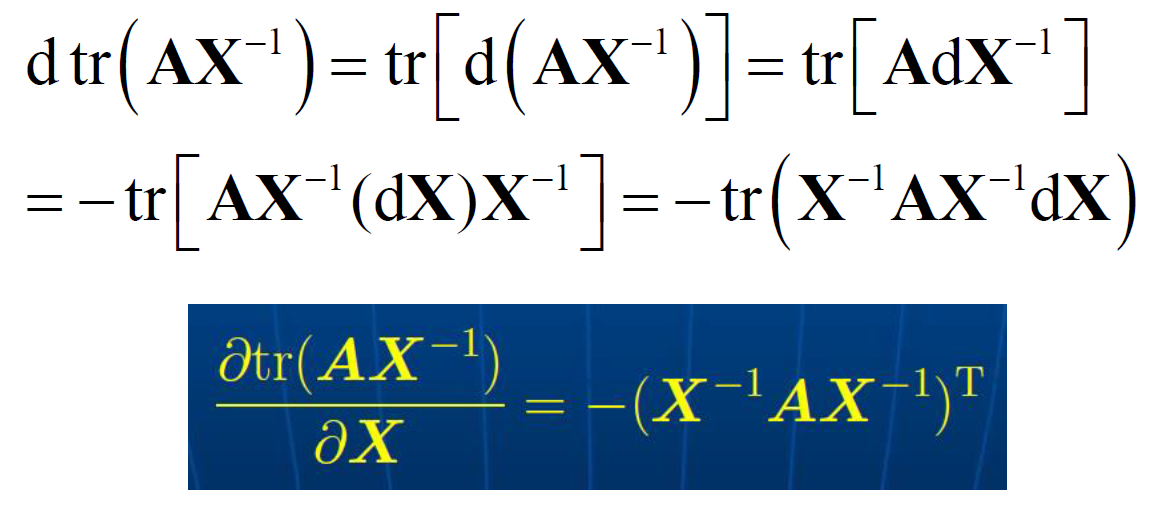
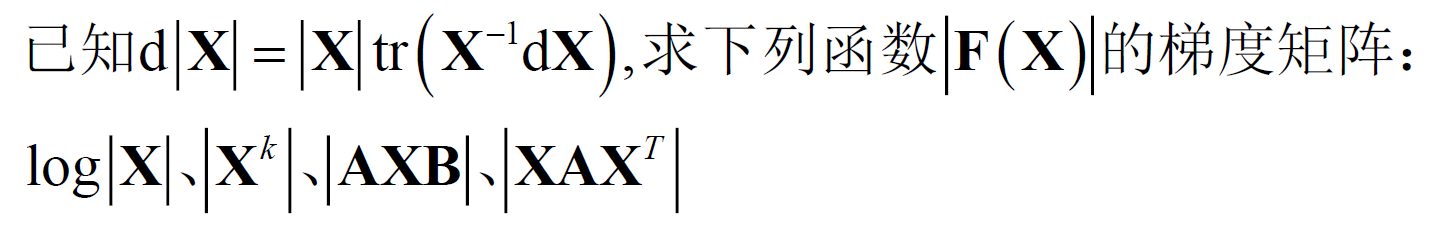
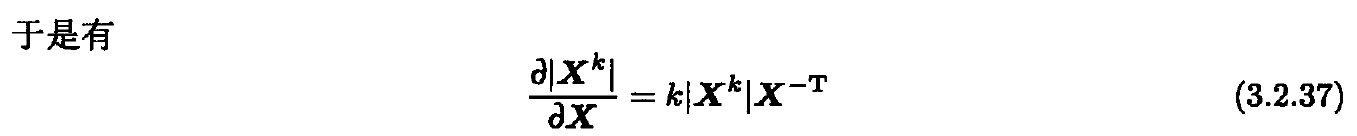
• 实值矩阵函数的Jacobin矩阵（重点）

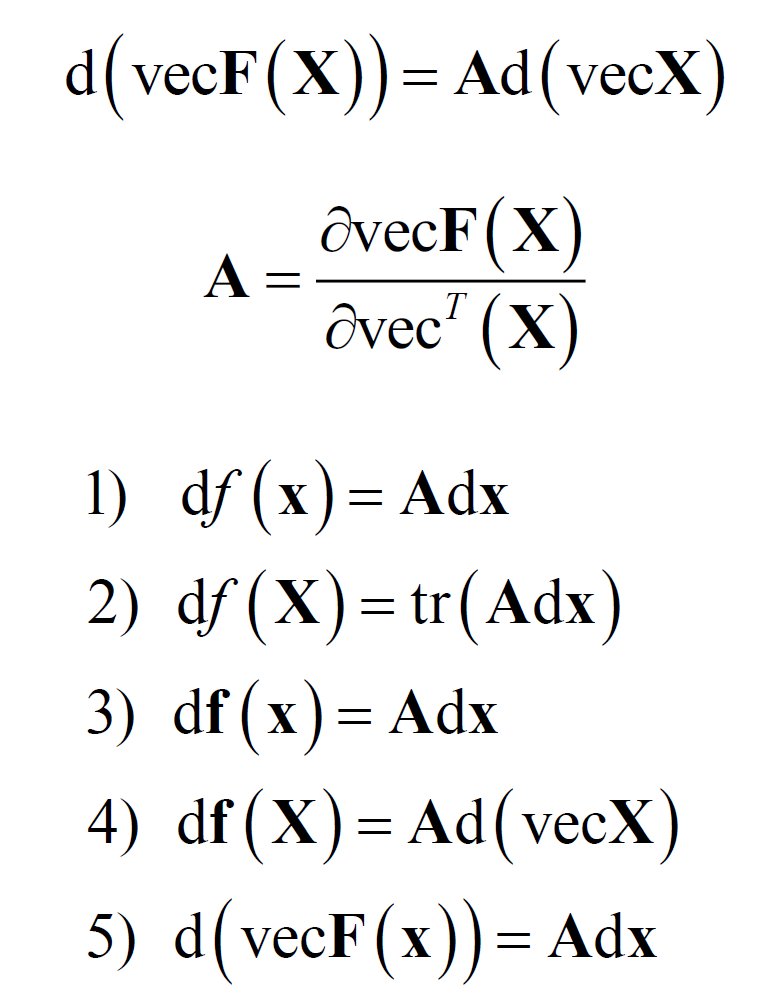
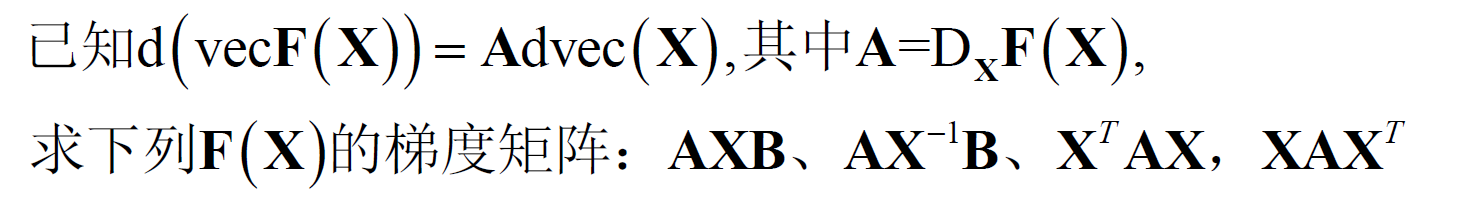
• 标量函数的Hessian矩阵。Hessian矩阵：多元函数的二阶偏导数构成的方阵。

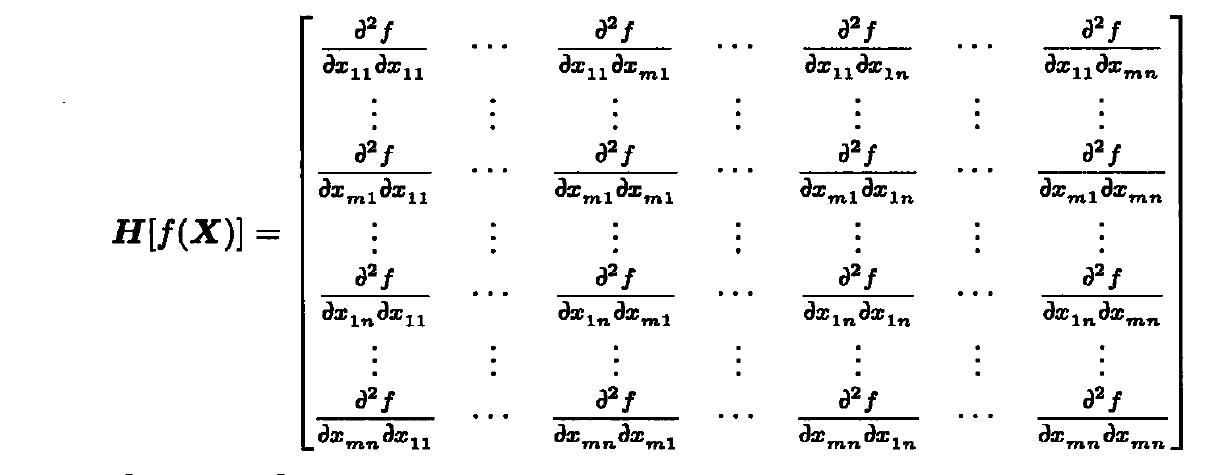
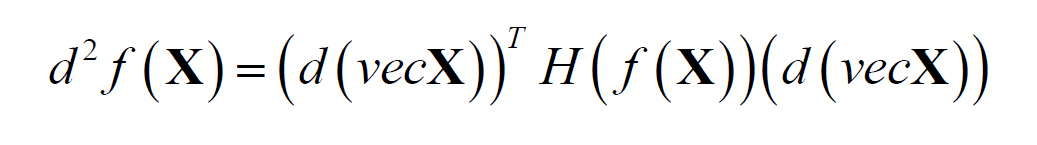
课后习题