signature-paper

Verifiable Timed Signatures Made Practical（实用的可验证的定时签名）

  定时签名是提交者在某消息上的签名，并与某个用户共享。经过一段时间T后，提交者向用户显示签名。如果提交者未能透露签名，则保证用户从最初给出的承诺中强制检索签名。

  本文中提出了可验证的定时签名（Verifiable Timed Signature：VTS），它让用户验证在𝐶中承诺的签名𝜎是否可以在时间T内通过ForceOp获得，并且确实是消息m的有效签名，即Vf(pk,𝑚,𝜎)=1。这种可验证性保证了用户能从承诺中获得一个有效的签名，且用户可以用ForceOp来检索。Commit额外输出一个证明𝜋，证明其嵌入的确实是消息m的签名。

  根据上述描述，我们给出可验证的定时签名算法，包括(Commit,Vrfy,Open,ForceOp)：

• (𝐶,𝜋)←Commit(𝜎,T) ：提交算法将签名𝜎 与隐藏时间T作为输入，并输出承诺𝐶和证明𝜋
• 0/1←Vrfy(pk,𝑚,𝐶,𝜋)：验证算法将公钥pk、消息𝑚, 承诺𝐶和证明𝜋作为输入，输出1时，当且仅当签名𝜎 嵌入到了承诺𝐶中，且签名𝜎 是消息𝑚的有效签名。
• (𝜎,𝑟)←Open(𝐶)：提交人将承诺𝐶作为输入，输出签名𝜎 以及用于生成承诺𝐶的随机数𝑟。
• 𝜎←ForceOp(𝐶)：强制开放算法将承诺𝐶 作为输入并输出签名𝜎。

   Soundness：在给定的承诺𝐶中，ForceOp算法将在时间T内产生承诺的签名𝜎。

   Privacy：所有运行时间最多为𝑡的算法（𝑡<T）都几乎不可能从承诺𝐶和签名𝜎中成功提取证明𝜋。

基础知识：

  数字签名。密钥生成算法KGen；签名算法Sign(sk, 𝑚)；验证算法Vf (pk, 𝑚, 𝜎) 。

  时间锁定难题（Time-Lock Puzzles）。时间锁定难题允许人们在一定的时间内隐藏一个值。直观地讲，时锁谜题保证了一个谜题可以在多项式时间内被解开，但是时间高于T。谜题生成PGen，它的输入是一个时间参数T，一个解𝑠和随机数𝑟，然后输出一个谜题𝑍。解题算法PSolve将一个谜题𝑍作为输入，并输出一个解决方案𝑠。在这种情况下，我们的敌手是并行随机存取机（Parallel Random Access Machines：PRAM），即多个处理器连接到一个内存块上，𝑛个数量的处理器可以同时对𝑛个数量的数据进行操作。

  同态时间锁难题（Homomorphic Time-Lock Puzzles：HTLP）。HTLP是由四种算法(HTLP.PSetup, HTLP.PGen,HTLP.PSolve, HTLP.PEval)组成的，其中HTLP.PGen与HTLP.PSolve和时间锁定难题类似，但是输入增加了公共参数𝑝𝑝。PSetup用于输出公共参数𝑝𝑝。PEval以电路𝐶，公共参数𝑝𝑝和𝑛个谜题𝑍1, . . ., 𝑍𝑛为输入，并输出谜题𝑍 ′，且满足HTLP.PSolve(𝑝𝑝,𝑍′)=𝐶(𝑠1,...,𝑠𝑛)，其中 𝑍′←HTLP.PEval(𝐶,𝑝𝑝,𝑍1,...,𝑍𝑛) 、𝑍𝑖←HTLP.PGen(𝑝𝑝,𝑠𝑖)。

  非交互式零知识证明。（1）ZKsetup进行初始化操作，该算法输出一个通用参考字符串crs。（2）ZKprove(crs, 𝑥, 𝑤)。验证者通过ZKprove来生成陈述x的证明𝜋，陈述x是由证人𝑤说的。（3）ZKverify(crs, 𝑥, 𝜋)。对陈述x的证明𝜋进行有效检查。

  BLS签名方案的VTS。密钥对为：(𝑔0^𝛼 , 𝛼)，g0是生成元。签名为𝜎=𝐻(𝑚)^𝛼。为了在消息m上生成VTS，将消息m的签名𝜎使用t-n方案进行共享。前面的t-1份签名碎片定义为𝜎_𝑖=𝐻(𝑚)^{𝛼_𝑖} 。之后的{t,t+1,...,n}份的签名碎片定义为：

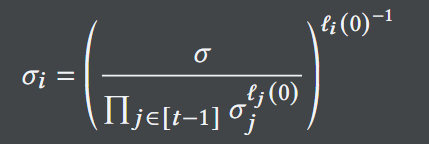
  其中，ℓ_𝑖()是𝑖-第三拉格朗日多项式基。相当于𝜎_i=H(m)^{𝛼-ℓ_1*𝛼_1-ℓ_2*𝛼_2-...-ℓ_{t-1}*𝛼_{t-1}}，其相当于公钥pk_i的签名，pk_i的定义如下：

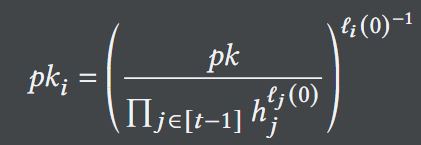
  相当于pk_i=g0^{𝛼-ℓ_1*𝛼_1-ℓ_2*𝛼_2-...-ℓ_{t-1}*𝛼_{t-1}}。

  这就保证了我们可以（通过拉格朗日插值）从任何𝑡个签名碎片中重建有效签名𝜎，也可以重构公钥pk。

  然后，承诺者为每个签名份额𝜎_i计算一个带有时间参数T的时间锁谜题𝑍_𝑖，得到所有谜题(𝑍_1,..., 𝑍_𝑛)和对应的公钥(pk_1,..., pk_𝑛)，这些信息作为承诺。然后，验证者随机选择一个大小为(𝑡-1)的集合𝐼。对于集合𝐼，承诺者打开时间锁谜题𝑍_𝑖,𝑖∈𝐼，得到了所承诺的信息𝜎_𝑖（以及相应的随机数）。如果满足以下所有条件，验证者认为承诺合法：

    （1）所有𝜎𝑖 ，𝑖∈𝐼都是有效的，即`𝑒(𝑔_0，𝜎𝑖)=𝑒(pk_𝑖,𝐻(𝑚))`。

    （2）所有公钥{𝑝𝑘_𝑗},𝑗∉𝐼可以重构公钥，得到pk。

  可以看到，如果不用PRAM，那么要解决n-t+1个时间锁难题（为什么不是n？后面会说），但是验证者如果利用PRAM，可以将验证时间缩短为T。但是对于处理器很少的诚实用户而言，验证耗时会很长，我们可以加入同态概念来解决这个问题。

  具体而言，验证者计算：

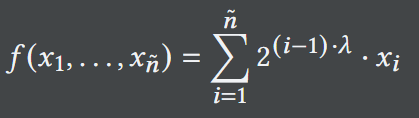
  从而将n-t+1个难题转化为1个难题，从而在时间T内解决这个难题。但是需要注意两点：(1) 同态时间锁谜题的信息空间必须大到足以容纳所有n-t+1个签名。(2) 输入谜题中编码的签名𝜎_𝑖不能超过签名的最大尺寸（例如𝜆比特）。第一点可以通过实例化足够大的消息空间来满足。第二点可以通过一个范围NIZK来执行，其规定每个时间锁谜题的消息都在[0, 2^𝜆]范围内。

  那我们如何实现一个范围NIZK呢？略。

实际构造：

  其中，t=n/2+1，H'是一个哈希函数，此哈希函数可以映射到一个t-1大小的集合，集合中的元素属于[1,2...,n]。

  Setup。运行ZKsetup，生成crs_range。运行HTLP.PSetup生成公共参数𝑝𝑝。生成crs=(crs_range,pp)。

  Commit and Prove。对于输入(crs, wit)，算法进行如下操作：

    （1）解析wit = 𝜎，crs= (crs_range, 𝑝𝑝)，pk为BLS公钥，𝑚为待签名信息。

    （2）选取t-1个𝛼_𝑖←Z_𝑞,𝑖∈[𝑡-1]，并设置𝜎_𝑖=𝐻(𝑚)^{𝛼_𝑖},ℎ_𝑖=𝑔0^{𝛼_𝑖} 。

    （3）对于𝑖∈{𝑡,...,𝑛}，计算：

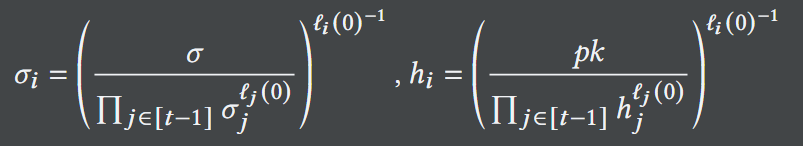
    （4）对于𝑖∈[1,...,𝑛]，产生谜题与NIZK：

    （5）计算：

    （6）输出承诺C与证明𝜋：

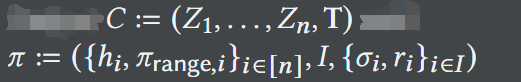
  Verification。将(crs,pk,𝑚,𝐶,𝜋)作为输入，进行验证算法：

    （1）解析𝐶=(𝑍_1,...,𝑍_𝑛,T),𝜋=({ℎ_𝑖,𝜋_{range},𝑖},𝐼,{𝜎_𝑖,𝑟_𝑖}),crs=(crs_{range},𝑝𝑝)。

    （2）如果满足以下任何条件，则输出0，否则返回1：

      a. 存在𝑗∉𝐼，有：

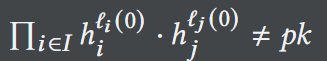
      b. 存在𝑖∈[𝑛]，有：

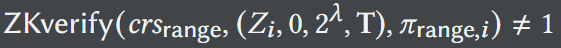
      c. 存在𝑖∈𝐼，有：

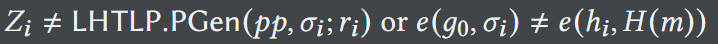
      d. 满足：

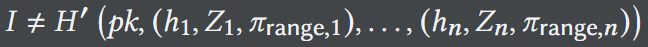
   Open。算法输出：

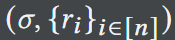
   Force Open。算法将𝐶=(𝑍_1,...,𝑍_𝑛,T)作为输入。

      （1）运行𝜎_𝑖←LHTLP.PSolve(𝑝𝑝,𝑍_𝑖),𝑖∈[1,..,𝑛]以获得所有签名。请注意，由于承诺者已经打开了𝑡-1个谜题，因此ForceOp只需要解决(𝑛-𝑡+1)个谜题即可。（利用同态）

      （2）输出签名：

Policy-Compliant Signatures（符合策略的签名：PCS）

  摘要：PCS的概念，即一个中央机构确定一个全局政策，并将与属性集相关的公私钥分配给系统中的用户。如果两个用户，Alice和Bob，拥有共同满足某个属性集，那么Alice可以使用她的私钥和Bob的公钥来签署一个信息。只有此属性满足策略时，才能产生一个有效的签名（不可伪造性，即使拥有私钥，但是如果发送方和接收方不满足策略，恶意发送方也不可能伪造有效签名）。且签名除了满足政策之外，不透露任何关于用户属性的信息（隐私性）。PCS扩展了基于属性的签名和基于政策的签名，最后本文描述了PCS的实际应用（在金融系统中控制具有强大隐私保证的交易）。

  如果某公司利用PCS用于生成签名，那么公司可以设置一个政策，限制谁可以向谁发送资金。具体来说，PCS方案允许中央机构针对某种策略生成主公钥和主密钥，并将主公/私钥发送给授权机构。然后，授权机构可以使用主公/私钥来生成与一组与属性相关联的公钥/私钥对。然后，签名者Alice使用其私钥和接收者Bob的公钥为消息创建签名。所有公钥都可以验证签名，且只有当Alice和Bob的属性共同满足全局策略时，它才有效。

  PCS的隐私性具体体现在：（1）外人只看到双方之间的公钥和签名，不应该了解这些方的属性。（2）发送者不应该了解接收者的属性，除非他们的属性是否满足策略。（3）接收者不应该了解发送者的属性，除非他们的属性是否满足策略。

PCS的构造

  PCS的一个简单实现：中央机构负责检查每一笔交易的合规性，确保每当具有属性x的发送方S向具有属性x^∗的接收方R发送消息时，F(x,x^∗)所规定的策略得到满足。虽然概念上很简单，但我们不想要中央机构，我们想让中央机构只用于发布证书。

  PCS的改进。授权机构向系统中的每个参与者发布密钥对(pk,sk)和相应属性证书C_x。为了发送消息m，发送方S对消息m进行签名，并使用NIZK证明发送方和接收方的证书所对应的属性满足策略F(x,x*)。但它要求发送方必须知道接收方的属性。

  那我们如何解决这个问题呢？（即发送方在不知道接收方属性的情况下生成一个NIZK证明，来证明发送方与接收方的属性均满足策略。）

  答案：使用谓词加密PE，谓词加密允许每个参与者在生成签名时只学习1 bit信息，此信息为F(x,x^*)。

PCS的应用

  （1）金融支付系统。区块链等服务。

  （2）信任谈判。情报交换，例如A要发机密消息给B，A使用B的公钥对消息M进行加密，并使用PCS方案对相应的密文进行签名（使用A的私钥和B的公钥）。如果生成的签名有效，则A将数据包发送给B，否则不发送消息。如果策略得到满足，那么B将知晓此消息。否则，B什么也得不到。

PCS介绍

  假设X_λ代表属性集，那么有谓词F:X_λ × X_λ→{0,1}，很多个F组成了谓词集。那么PCS由四个算法组成：

      Setup。输入安全参数λ与策略（谓词）F，输出主公私钥(mpk,msk)。

      KeyGen。输入msk与一组属性x∈X_λ，输出公私钥(pk,sk)。

      Sign。输入为主公钥mpk，发送者私钥sk_S，接收者公钥pk_R与消息m，输出签名σ或⊥。

      Verify。输入为主公钥mpk，发送者公钥pk_S，接收者公钥pk_R、消息m与签名σ，输出0或1。

  PCS的正确性定义为：

  敌手在安全游戏中的能力

    敌手可以控制很多预言机。例如，敌手可以使用预言机QKeyGen或QKeyGenLR获得所选属性的公钥；敌手可以使用预言机QCor获得与给定公钥对应的私钥；使用QSign获得与所选公钥相关的签名。分别如下：

    （1）Key-Generation Oracle QKeyGen：给定一组属性x_i，生成(pk_i,sk_i)←KeyGen(msk,x_i)，将(i,pk_i,sk_i,x_i)添加到QK集合中，并返回pk_i。

    （2）Left-or-Right Key-Generation Oracle QKeyGenLR：对于第i次输入的一组属性x_{i,0}与x_{i,1}，生成(pk_i,sk_i)←KeyGen(msk,x_{i,β})，其中β是安全游戏中选择的比特。将(i,pk_i,sk_i,x_{i,0},x_{i,1})添加到QK集合中，并返回pk_i。

    （3）Corruption Oracle QCor：输入索引i，如果QK中包含含有i的条目，那么就将该条目放入集合QC中，并返回私钥sk_i，否则返回⊥。

    （4）Signing Oracle QSign：输入索引i（对应发送者），公钥pk'（对应接收者）与消息m，如果QK包含i的条目，那么就返回σ←PCS.Sign(mpk,sk_i,pk',m)，并将(i,pk_i,pk',m,σ)添加到QS中。

  存在不可伪造性

  Indistinguishability-Based Attribute Hiding（基于模糊性的属性隐藏）